Géométrie dans l'espace

par **missti** » 01 Juin 2009, 09:24

Bonjour à toi aussi,

Soit M(0;3;4) N(3;0;2) et L(0;0;4)
A quel plan de base appartiennent les points N et L ?
Dans ce plan, déterminer l'équation réduite de la droite (LN)
En déduire une équation de plan P parallèle à (Oy) et passant par L et N.
Justifier que M est un point du plan P.

( Voilà l'exercice ceci-dit si vous pouviez m'expliquer comment faire car j'ai étais absente durant le cours et j'ai réellement du mal à rattraper cela m'aiderait beaucoup je vous remercie d'avance :happy2: )

par **Ericovitchi** » 01 Juin 2009, 09:32

Regardes tes deux points N et L ou mieux dessines les. Que remarques tu ? Ne trouves tu pas un plan de base dans lequel ils sont tous les deux ?

par **Cheche** » 01 Juin 2009, 09:32

Salut à toi Missti.

Question 1:
La première question est un peu particulière car il faut comprendre le terme "plan de base".

Mais leurs définitions me paraissent intuitives.
Soit un repère (O,x,y,z).

Les plans de base sont (O,x,y), (O,x,z) et (O,y,z).

Maintenant à toi de trouver la particularité des points N et L et tu trouveras facilement dans quel plan de base, ils se trouvent.

Remarque : Tu peux me donner les équations des plans : (O,x,y), (O,x,z) et (O,y,z)

Question 2 :
La droite LN est incluse dans le plan de base de L et de N. Donc les points de (LN) respectent l'équation du plan de base.

Mais pour définir une droite en 3 Dimensions, on a besoin de deux équations.
Pour la trouver, tu te places dans le plan de base et tu fais le même raisonnement qu'un deux dimension. (ax+by+c=0 etc ...)

Attention : Je dis ax+by+c=0 mais ça peut être ax+bz+c=0

Question 3:

par **missti** » 01 Juin 2009, 09:48

Bonjour, Alors j'ai suivi du moins essayer de suivre vos deux explications.
Je trouve N appartient au plan de base (Oxy) et L appartient au plan de base(Ozy) ce qui ne me parait pas logique puisque la question regroupe les deux points je devrais normalement trouver le même plan de base :doh:

par **Ericovitchi** » 01 Juin 2009, 09:58

Je trouve N appartient au plan de base (Oxy)

non, N(3;0;2), s'il était sur Oxy, son z serait égal à zéro !

par **missti** » 01 Juin 2009, 10:05

Bon les points N et L appartiennent au plan de base (Oyz).
Pour l'équation réduite de la droite (LN) je fais donc ay+bz+c=0 ?

par **Cheche** » 01 Juin 2009, 10:33

Non,

As tu fait un schéma en plaçant les trois points ?
Voix tu à quoi ressemble les trois plans ?

Le plan de base : (O,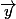

,

)
est l'ensemble des points M tel que il existe a et b :

Donc ce plan a pour équation : y = 0

Pour répondre aux questions de l'exercice, tu as deux solutions :

- tu fais un schéma et tu trouves la solution sur le schéma.
ou
- tu écris les équations de plan et tu en déduits qui appartient à quoi.

par **Ericovitchi** » 01 Juin 2009, 11:02

Bon les points N et L appartiennent au plan de base (Oyz).
Pour l'équation réduite de la droite (LN) je fais donc ay+bz+c=0 ?

Non, comme l'a dit Cheche les deux points ont pour caractéristique commune y=0 donc ils sont dans (Oxz) donc ta droite a une équation ax+bz+c=0 dans le plan (Oxz) (si tu avais fait un dessin, tu l'aurais vu graphiquement)
Pour trouver a,b,c il faut remplacer les coordonnées des points dans l'équation et résoudre le système.

par **missti** » 03 Juin 2009, 12:11

Merci de toutes vos réponses
Bien que je n'ai toujours pas réussi à finir cet exercice le début a était compris et c'est déjà cela de gagné :)

par **missti** » 03 Juin 2009, 13:16

Merci merci merci !
J'avais fais une erreur dans mon schéma ce qui faussait tout mais grâce à vos explications j'ai trouvé mon erreur et je peux enfin re-commencer mon exercice en étant beaucoup moins stressé ^^ :++:

par **missti** » 03 Juin 2009, 14:21

Je l'ai enfin terminé ça a prit du temps mais ça valait le coup étant donné que j'ai réussi Merci ce ne serait pas arrivé sans vous

Géométrie dans l'espace

Géométrie dans l'espace

Qui est en ligne