Olympiades/exercice 2

par **kasmath** » 30 Mai 2009, 18:08

salut
soit

trois nombre rèel verifier

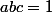
montrez que

par **sniperamine** » 30 Mai 2009, 20:28

kasmath a écrit:salut
soit trois nombre rèel verifier
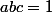
montrez que

où est la politesse ? tu poses tes exo et tu disparais bof bof bof

par **kasmath** » 30 Mai 2009, 20:41

sniperamine a écrit:où est la politesse ? tu poses tes exo et tu disparais bof bof bof

je suis toujour la avec vous*

par **Imod** » 30 Mai 2009, 21:38

kasmath a écrit:je suis toujour la avec vous*

D'accord mais tu proposes des exercices en continu sans jamais prendre la peine de d'affirmer ou d'infirmer les réponses qu'on te fournit : drôle de conception d'une participation à un forum :triste:

Imod

par **bikerj2009** » 31 Mai 2009, 12:19

kasmath a écrit:salut
soit trois nombre rèel verifier
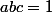
montrez que

pr repondre à ta question j'ai une seule solution:
on sait ke abc=1,alors si je prends a=1;b=1 et c=1 si je me trompe pas ça resoud ton enigme.

par **sniperamine** » 31 Mai 2009, 12:21

bikerj2009 a écrit:pr repondre à ta question j'ai une seule solution:
on sait ke abc=1,alors si je prends a=1;b=1 et c=1 si je me trompe pas ça resoud ton enigme.

Chapeau bas :id:

par **Zweig** » 31 Mai 2009, 12:22

Sauf qu'il existe une infinité de réel vérifiant abc = 1. Pour preuve : x/y*y/z*z/x = 1 pour tout (x,y,z). Tu ne montres que c'est vrai que dans un cas très particulier.

par **bikerj2009** » 31 Mai 2009, 12:23

kasmath a écrit:je suis toujour la avec vous*

si tu est rellement là daigne au moins par politesse dire si la proposition ta éclairé.

par **bikerj2009** » 31 Mai 2009, 12:26

Zweig a écrit:Sauf qu'il existe une infinité de réel vérifiant abc = 1. Pour preuve : x/y*y/z*z/x = 1 pour tout (x,y,z). Tu ne montres que c'est vrai que dans un cas très particulier.

cela n'est pas faux mais dans ce cas précis la solution la plus probable est le triplet (1,1,1).

par **lapras** » 31 Mai 2009, 12:27

Peut etre as tu montré par un lissage qu'on peut se rammener au cas a=b=c ?

par **sniperamine** » 31 Mai 2009, 12:27

bikerj2009 a écrit:cela n'est pas faux mais dans ce cas précis la solution la plus probable est le triplet (1,1,1).

Désolé mais tu dis n'importe quoi . Tu dois montrer l'inégalité pour tout a;b;c

par **bikerj2009** » 31 Mai 2009, 12:27

sniperamine a écrit:Chapeau bas :id:

sois plus explicite!

par **bikerj2009** » 31 Mai 2009, 12:30

sniperamine a écrit:Désolé mais tu dis n'importe quoi . Tu dois montrer l'inégalité pour tout a;b;c

si c'est rellement du n'importe quoi donne donc une réponse cela m'apprendra à mieu répondre la prochaine fois.

par **sniperamine** » 31 Mai 2009, 12:33

Sans rancune; tu ne dois pas prendre des cas particuliers et désolé pour mon "n'importe quoi " je voulais pas dire ça

par **bikerj2009** » 31 Mai 2009, 12:36

sniperamine a écrit:Désolé mais tu dis n'importe quoi . Tu dois montrer l'inégalité pour tout a;b;c

en effet tu as raison mais dans un autre cas ce n'est pas tjrs vérifié.

Olympiades/exercice 2

olympiades/exercice 2

proposition de solution

Qui est en ligne