Démo erronée
Olympiades mathématiques, énigmes et défis
-
Yawgmoth
- Membre Relatif
- Messages: 206
- Enregistré le: 06 Jan 2007, 23:17
-
 par Yawgmoth » 24 Mai 2009, 21:53
par Yawgmoth » 24 Mai 2009, 21:53
Bonsoir,
Il se trouve qu'en parcourant un peu le net, je suis tombé sur cette démonstration :
Étape 1 : partons de l'équation suivante :
x²+ x + 1 = 0 (1)
Étape 2 : écrivons cette équation sous la forme
x + 1 = - x² (2)
Étape 3 : reprenons l'équation (1) et écrivons-là sous la forme
x(x+1)+1 = 0 (3)
Étape 4 : remplaçons dans l'équation (3) le facteur x+1 par sa valeur trouvée par l'équation (2)
x(-x²)+1 = 0 (4)
Étape 5 : soit en réécrivant cette équation (4)
-x³+1 = 0 (5)
Étape 6 : ou encore x³= 1 (6)
Étape 7 : d'où on en déduit la solution x = 1 (7)
Étape 8 : en remplaçant cette solution dans l'équation (1) de départ, on obtient bien :
1+1+1 = 0 soit 3 = 0 !
Qu'en pensez-vous ? :zen:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Mai 2009, 22:05
par Nightmare » 24 Mai 2009, 22:05
Bonsoir,
Déjà discuté de nombreuses fois. L'étape 7 est fausse pour une raison évidente, la même qui fait que la démonstration suivante est idiote :
"S'il pleut, il y a des nuages gris, s'il y a des nuages gris le ciel est sombre. Chaque nuit le ciel est sombre donc chaque nuit il pleut".
:happy3:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 24 Mai 2009, 22:13
par Timothé Lefebvre » 24 Mai 2009, 22:13
Bonsoir,
dès le départ, en voulant résoudre ce polynôme on admet qu'il y a au moins une racine réelle, ce qui n'est pas le cas ...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Mai 2009, 22:19
par Nightmare » 24 Mai 2009, 22:19
Timothé Lefebvre a écrit:Bonsoir,
dès le départ, en voulant résoudre ce polynôme on admet qu'il y a au moins une racine réelle, ce qui n'est pas le cas ...
Non, les étapes 1 à 6 sont exactes.
-
Yawgmoth
- Membre Relatif
- Messages: 206
- Enregistré le: 06 Jan 2007, 23:17
-
 par Yawgmoth » 24 Mai 2009, 22:19
par Yawgmoth » 24 Mai 2009, 22:19
Ah je m'excuse si cela a déjà été discuté.
Par contre désolé mais pourquoi l'étape 7 est mauvaise ?
Si x³ = 1, alors x = 1 non ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 24 Mai 2009, 22:21
par Timothé Lefebvre » 24 Mai 2009, 22:21
Dans ce cas la racine cubique de 1 dans

est bien 1, et donc qu'est-ce qui permet de dire que la 7 est mauvaise ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 24 Mai 2009, 22:23
par Timothé Lefebvre » 24 Mai 2009, 22:23
De toute façon le simple calcul du discriminant nous montre que le résultat est absurde, donc pas besoin de débattre de ce raisonnement qui se base sur le fait qu'on va trouver une solution alors qu'il n'y en a pas.
-
Yawgmoth
- Membre Relatif
- Messages: 206
- Enregistré le: 06 Jan 2007, 23:17
-
 par Yawgmoth » 24 Mai 2009, 22:24
par Yawgmoth » 24 Mai 2009, 22:24
Ah donc dire ça suffit. Chouette parce que je trouvais pas autre chose :mur: :mur: :we: .
Merci beaucoup pour vos réponses.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Mai 2009, 22:37
par Imod » 24 Mai 2009, 22:37
Je trouve plutôt intéressants ces exercices ou tout est dans ce que l'on dit ou ne dit pas : si l'équation initiale a une solution dans R , dans C ou ailleurs , alors

. La solution réelle

de

n'est pas solution de l'équation initiale et alors , jamais il n'a été dit que les équations écrites étaient équivalentes .
Imod
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 25 Mai 2009, 00:22
par Quidam » 25 Mai 2009, 00:22
Je pense que la seule chose qui est fausse dans cette démonstration est le mot "la" dans "on en déduit la solution x=1".
Il fallait plutôt dire (pour quelqu'un qui ne connaît que les réels) "on en déduit que la seule solution possible ne peut être que 1". L'étape 8 constate simplement que 1 n'est pas solution du problème, et comme c'était la seule possible c'est qu'il n'y a pas de solution ! Il n'y a aucun paradoxe !
Cette "énigme" est évidemment destinée à un lycéen qui n'a connu que les réels et qui de préférence n'a jamais étudié les trinômes du second degré. Il n'y a pas de faute dans l'implication : "x²+x+1 entraîne

=1". Elle est parfaitement correcte. S'il existe une solution alors elle vérifie

; c'est inattaquable !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Mai 2009, 00:25
par Nightmare » 25 Mai 2009, 00:25
Timothé Lefebvre a écrit:De toute façon le simple calcul du discriminant nous montre que le résultat est absurde, donc pas besoin de débattre de ce raisonnement qui se base sur le fait qu'on va trouver une solution alors qu'il n'y en a pas.
Justement, débat il doit y avoir. Ce faux problème est intéressant car il soulève une erreur que 99% des élèves font : confondre une implication et une équivalence.
Ce problème se rencontre au lycée principalement avec les équations et cette énigme en témoigne parfaitement, la preuve étant, quasiment aucun lycée n'arrive à déceler l'erreur dans ce raisonnement et pire que ça, il leur parait complètement logique.
Pourtant, si j'écris : " Supposons que x=1, alors x²=1 et donc x=1 ou -1. En particulier -1=1" cela parait complètement idiot alors que c'est la même erreur.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Mai 2009, 00:27
par Nightmare » 25 Mai 2009, 00:27
Quidam a écrit:Je pense que la seule chose qui est fausse dans cette démonstration est le mot "la" dans "on en déduit la solution x=1".
Il fallait plutôt dire (pour quelqu'un qui ne connaît que les réels) "on en déduit que la seule solution possible ne peut être que 1". L'étape 8 constate simplement que 1 n'est pas solution du problème, et comme c'était la seule possible c'est qu'il n'y a pas de solution ! Il n'y a aucun paradoxe !
Cette "énigme" est évidemment destinée à un lycéen qui n'a connu que les réels et qui de préférence n'a jamais étudié les trinômes du second degré. Il n'y a pas de faute dans l'implication : "x²+x+1 entraîne

=1". Elle est parfaitement correcte. S'il existe une solution alors elle vérifie

; c'est inattaquable !
Dans ce cas là, ce n'est pas le "la" qui dérange mais le "on en déduit" et le mot important dans ta correction est "possible".
-
melreg
- Membre Relatif
- Messages: 325
- Enregistré le: 10 Déc 2007, 20:09
-
 par melreg » 25 Mai 2009, 08:47
par melreg » 25 Mai 2009, 08:47
Pour appuyer les dires de Imod et Nightmare (je trouve que ton dernier exemple montre bien et de manière simple le problème): on remarque que
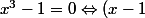(x^2+x+1)=0)
Et donc, dans les implications des étapes 1-4 on a élevé le degré de l'équation, et effectivement on a "ajouté" une solution. On voit clairement que SI

est solution de
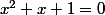
, ALORS il est solution de
(x^2+x+1)=0)
donc de

. L'implication inverse est fausse...
Dans la déduction finale, on ne garde que la "solution" qui embête, et on ne tient plus compte des deux autres (qui elles sont évidemment solutions de l'équation de départ). Pour un exemple plus simple, il faut regarder celui de Nightmare.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
