Probleme argument module

[manianga]

bonjour tout le monde pourriez vous m'aider pour ces exercices svp?

avec z un nombre complexe de partie réelle a et imaginaire b

determiner le module de

z²; z+1; 2z-1;(z+i)(2z-1)

mon probleme c'est que comme j'ai été absent je ne vois pas comment faire et j'ai beau chercher dans mon livre je ne trouve pas d'explications.

ensuite je dois determiner un argument de

-2/3; 5+5i;-1-i; 8i/7

merci pour vos reponses

[tigri]

bonjour

un complexe s'écrit a+bi ,où a est la partie réelle , et b la partie imaginaire : a et b sont des réels

le module d'un complexe c'est |z|= rac(a²+b²)
il représente la longueur OM, si M représente le point image de z : M(a,b)

[julian]

Bonjour,
Comme tu as été absent, je vais simplement te donner les formules pour que tu puisses t'entraîner (on reste là si tu a besoin d'une vérification :++:)
tu as z=a+ib

Le module se calcul avec la formule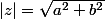

Et l'argument il faut que tu calcules : et et que tu en déduises l'argument.
Je vais te donner un exemple: si tu trouve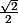 pour les 2 , c'est que l'argument vaut , si tu trouves , et c'est que l'argument vaut , etc...

Après il y a des règles pour les modules et les argument:
|z²|=|z|²
|kz|=k|z|
|zz'|=|z|x|z'|

Et pour les arguments tu as entre autres:
et argzz'= argz+argz'.

Voilà tu ne devrais pas en avoir besoin de plus, mais c'est très étrange que tu ne trouves rien dans ton bouquin... :mur:

[manianga]

donc si j'ai bien saisi

le module de z² c'est racine de (a²+b²)²
|z+1|=a+b+1
|2z-1|= 2a+2b-1
par contre le dernier je ne vois pas comment faire

[ParLaLaSortie]

Attention,

si z = a + ib, tu as , puis
z+1 = (a+1) + ib donc et non pas a + b+ 1 etc.

[manianga]

pour les arguments

-2/3 je trouve pi +2kpi
5+5i pi/4+2kpi
-1-i -pi/4 +2kpi
8i/7 pi/2 +2kpi

ca a l'air bon ?

[fonfon]

Salut, je trouve

-2/3 pi +2kpi
5+5i pi/4+2kpi
-1-i -3pi/4 +2kpi
8i/7 pi/2 +2kpi