Bonjour ,
Qlq'un pourrait'il m'aider pr cet exo (..2)a)etb) ...) svp
ABCD est un carré de coté 4.
I désigne le milieu du segment [AD] et J est le milieu du segment [BC].
M et N sont des points respectivement situés sur les segments [AD] et [IJ] tels que AM=JN .
On pose AM = x
1) Démontrer que IM2=(x-2)2. (il y a 2 cas a considerer)
je trouve le premier :
M entre A et I
IM=(x-2) donc IM2=(x-2)2
M entre I et D ..
2)Exprimer MN2 en fonction de x .
je trouve : theoreme de pythagore pr le triangla NIM
MN2=IM2+IN2
MN2=(x-2)2+(4-x)2
MN2= 2x2-12x+20
A partir de là , je ne comprends pas grand chose ..qlq'un peut 'il m'expliquer ??
3) Soit f la fonction définie sur R par f(x)=x2-6x+10
a)etudier les variations de f et dresser son tableau de variations
b)Le plan est rapporté à un repere orthogonal (O,v(vecteur)i , vj).Montrer que le droite d'équation x=3 est un axe de symetrie de la courbe representative de f .
c)Tracer cette courbe
Voila , merci d'avance
1 ere ..
9 messages
- Page 1 sur 1
Bonjour,
C'est bien la question 3/ que tu ne comprends pas?
Si c'est bien cela as-tu vu les dérivées? Alors je vais te donner des pistes et demande si tu as besoin de plus d'explication :++: :
a) pour étudier les variations d'une fonction sur un intervalle I il faut calculer sa dérivée et étudier le signe de cette dérivée. Si la dérivée est négative sur un intervalle de I, alors la fonction est décroissante sur cet intervalle. Si la dérivée est nulle sur un intervalle de I, alors la fonction est constante sur cet intervalle.Si la dérivée est positive sur un intervalle de I, alors la fonction est croissante sur cet intervalle.
Dans tableau tu mettras donc 3 lignes: une ligne avec les valeurs de x, 1 ligne avec les signes de la dérivée1 et 1 ligne avec les variations de la fonction
b) si la droite d'équation x=a est axe de symetrie de la fonction f, alors f(a+h)=f(a-h), et réciproquement. Calcule donc f(3+h) et f(3-h) et tu devrais trouver la même chose.
c) à tes crayons! :ptdr:
C'est bien la question 3/ que tu ne comprends pas?
Si c'est bien cela as-tu vu les dérivées? Alors je vais te donner des pistes et demande si tu as besoin de plus d'explication :++: :
a) pour étudier les variations d'une fonction sur un intervalle I il faut calculer sa dérivée et étudier le signe de cette dérivée. Si la dérivée est négative sur un intervalle de I, alors la fonction est décroissante sur cet intervalle. Si la dérivée est nulle sur un intervalle de I, alors la fonction est constante sur cet intervalle.Si la dérivée est positive sur un intervalle de I, alors la fonction est croissante sur cet intervalle.
Dans tableau tu mettras donc 3 lignes: une ligne avec les valeurs de x, 1 ligne avec les signes de la dérivée1 et 1 ligne avec les variations de la fonction
b) si la droite d'équation x=a est axe de symetrie de la fonction f, alors f(a+h)=f(a-h), et réciproquement. Calcule donc f(3+h) et f(3-h) et tu devrais trouver la même chose.
c) à tes crayons! :ptdr:
OUi désolé! :ptdr:
Et bien à ce niveau il y a beaucoup plus simple en fait!! (quoique tu verras que les dérivées sont un automatisme après...
Tu dois avoir quelque part dans ton cours: La courbe d'équation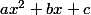 , avec a différent de 0 dans un repère (O;i;j) est une parabole dont le sommet a pour abscisse
, avec a différent de 0 dans un repère (O;i;j) est une parabole dont le sommet a pour abscisse  et pour ordonnée
et pour ordonnée  . Et d'autre part tu sais que la courbe est du signe de a à l'extérieur des racines (s'il le trinôme en a), et du signe de -a à l'intérieur des racines (s'il en a ^^). Et encore d'autre part tu sais que si a>0, la parabole "tend ses bras vers la haut", et si a0, f(x) est strictement positive.
. Et d'autre part tu sais que la courbe est du signe de a à l'extérieur des racines (s'il le trinôme en a), et du signe de -a à l'intérieur des racines (s'il en a ^^). Et encore d'autre part tu sais que si a>0, la parabole "tend ses bras vers la haut", et si a0, f(x) est strictement positive.
D'autre part, comme a>0 la parabole a ses "bras tendus vers le haut". Si tu te représentes cette parabole tu verras qu'elle atteint un minimum (qui est soon sommet) , qu'elle est décroissante avant ce minimum et croissant après (puisqu'elle a ses bras tendus vers le haut).
L'abscisse de son sommet est : son ordonnée est:
son ordonnée est:  . (si tu as une calculatrice graphique tu peux vérifier.
. (si tu as une calculatrice graphique tu peux vérifier.
Donc en gros ton tableau se résume comme çà:
une ligne avec les valeur de x suivante: , 3 et
, 3 et 
une grosse ligne avec les variations de f: décroissante sur et croissante sur
et croissante sur  (et tu mets l'ordonnée 1 entre les deux flèches)
(et tu mets l'ordonnée 1 entre les deux flèches)
Voilà j'espère avoir été assez clair, parce si çà a pu t'aider et si tu as compris çà te sera très utile. :++:
Amicalement.
Et bien à ce niveau il y a beaucoup plus simple en fait!! (quoique tu verras que les dérivées sont un automatisme après...
Tu dois avoir quelque part dans ton cours: La courbe d'équation
D'autre part, comme a>0 la parabole a ses "bras tendus vers le haut". Si tu te représentes cette parabole tu verras qu'elle atteint un minimum (qui est soon sommet) , qu'elle est décroissante avant ce minimum et croissant après (puisqu'elle a ses bras tendus vers le haut).
L'abscisse de son sommet est :
Donc en gros ton tableau se résume comme çà:
une ligne avec les valeur de x suivante:
une grosse ligne avec les variations de f: décroissante sur
Voilà j'espère avoir été assez clair, parce si çà a pu t'aider et si tu as compris çà te sera très utile. :++:
Amicalement.
Merciiiiiiiiiiiiiiiiiiiiiiiiiii julian ....j' ai "presque" tt compris ..mais j'ai des soucis pr faire le tableau ...je ne sais pas ou plutot plus comment faire ...(blocage) ..je sais , c'est grave ..!!..mais bon , je ne suis pas une bosse en math !! =)=)=)
merci encore .
[img]....-infini......3......+infini[/img]
[img]x.......%20\%20..............>[/img]
[img]...........>....1....%20/[/img]
si tu comprends ..t'es fort !! ..si , oui ...c'est bon ou pas ??les fleches sont bizarre mais je ne sais pas comment faire autrement ..
merci =)
merci encore .
[img]....-infini......3......+infini[/img]
[img]x.......%20\%20..............>[/img]
[img]...........>....1....%20/[/img]
si tu comprends ..t'es fort !! ..si , oui ...c'est bon ou pas ??les fleches sont bizarre mais je ne sais pas comment faire autrement ..
merci =)
Oui c'est parfait (j'ai compris!!!! :ptdr: ) . Mets peut-être  et
et  en haut des 2 flèches dans la ligne des variations, mais sinon c'est niquel.
en haut des 2 flèches dans la ligne des variations, mais sinon c'est niquel.
Bonne continuation. :++:
ps: le x qu'il y a dans la ligne variation n'a rien a y faire par contre, mais je pense que c'est à cause de la bizarrerie du tableau . :++:
Bonne continuation. :++:
ps: le x qu'il y a dans la ligne variation n'a rien a y faire par contre, mais je pense que c'est à cause de la bizarrerie du tableau . :++:
Re-bonjour,
La fonction x-> MN² est la fonction x->2x²-12x+20 .
Or ne remarques-tu pas que les coefficients de cette fonction sont multipliés par 2 par rapport à ceux de la fonction f?
Pour trouver la valeur de x minimale, c'est la même chose: il faut trouver les variations de f, et cette valeur de x c'est l'abscisse du sommet de la fonction (si elle a les branches tournées vers le haut bien sur). Mais agis judicieusement car vu qu'il n'y a qu'un coefficient 2 qui change d'une fonctiuon à l'autre, donc un tas de calculs pourraient être évités. :++:
ps: Dans mon plus grand message, il y avait écrit:
"Donc en gros ton tableau se résume comme çà:
une ligne avec les valeur de x suivante: f(x)=x², 3 et "
"
Mais c'est bien sûr , 3 et
, 3 et  (j'ai modifié ^^).
(j'ai modifié ^^).
Bye.
La fonction x-> MN² est la fonction x->2x²-12x+20 .
Or ne remarques-tu pas que les coefficients de cette fonction sont multipliés par 2 par rapport à ceux de la fonction f?
Pour trouver la valeur de x minimale, c'est la même chose: il faut trouver les variations de f, et cette valeur de x c'est l'abscisse du sommet de la fonction (si elle a les branches tournées vers le haut bien sur). Mais agis judicieusement car vu qu'il n'y a qu'un coefficient 2 qui change d'une fonctiuon à l'autre, donc un tas de calculs pourraient être évités. :++:
ps: Dans mon plus grand message, il y avait écrit:
"Donc en gros ton tableau se résume comme çà:
une ligne avec les valeur de x suivante: f(x)=x², 3 et
Mais c'est bien sûr
Bye.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
