Nightmare a écrit:Le résultat étant vrai, trouver un contre exemple risque d'être ardu !
Je parlais d'un contre exemple dans le cas où l'on prendrait un ouvert qui n'est pas un disque.
Hmm, la mesure donc. Ok, merci.
Edit : la mesure est invariante par rotation.
Soit R la rotation de centre

et d'angle

. Pour

harmonique,
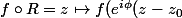))
est encore harmonique (ça se calcule simplement).
Ainsi l'intégrale de

sur

, vaut
-d'une part
f(z_0))
(par invariance de la mesure par rotation et car
=z_0)
), donc aussi l'intégrale de

sur

;
-d'autre part vaut l'intégrale de

sur
)
On a donc prouvé que l'intégrale de

est identique sur tout ouvert obtenu en tournant l'ouvert initial autour de

.
Reste à savoir si c'est suffisant pour conclure :marteau:
Si maintenant cet ouvert n'est pas un disque, alors par ces rotations on peut obtenir deux ouverts différents.
(Edit : Attention, ceci est faux, puisque les couronnes sont un contre-exemple... Ou encore tout ce qu'on peut obtenir en soustrayant à un disque des disques ou des cercles concentriques : mais apparemment, le résultat est encore vrai pour eux (se référer à mon calcul page précédente, on intègre ici sur r entre disons r1 et r2, c'est comme intégrer sur 0...r2 et soustraire l'intégrale sur 0...r1, on sait calculer ces deux intégrales par la formule de la moyenne, et on tombe bien sur l'aire de la couronne...)) Dans le cas où l'ouvert n'est pas invariant par toutes les rotations (cf mon post suivant) il nous suffit maintenant de construire une fonction harmonique telle que les intégrales sur deux tels ouverts ne soient pas identiques. Ce qui doit bien exister...
Par exemple, prendre

positive, et étant donné un disque
 \subset R(\Omega))
, prendre

telle que
)
soit assez grand pour que :
} f \geq \Pi r_1^2 f(z_1))
soit

Reste à construire une telle fonction :marteau: