Dm nombre d'or
13 messages
- Page 1 sur 1
dm nombre d'or
bonjour à tous,
j'ai un devoir maison a faire pour lundi 29 mai
et je bloque sur la première partie
pourriez vous m'expliquer s'il vous plait ?
merci beaucoup
flohttp://www.pedagogie.ac-nantes.fr/1209803343570/0/fiche___ressourcepedagogique/&RH=MATH
j'ai un devoir maison a faire pour lundi 29 mai
et je bloque sur la première partie
pourriez vous m'expliquer s'il vous plait ?
merci beaucoup
flohttp://www.pedagogie.ac-nantes.fr/1209803343570/0/fiche___ressourcepedagogique/&RH=MATH
flower85 a écrit:bonjour à tous,
j'ai un devoir maison a faire pour lundi 29 mai
et je bloque sur la première partie
Salut,
on part de
tout nombre quadratique se développe en fraction continue:
(cf "Duverney théorie des nombres" chez Dunod)
ça , ça peut se vérifier en 3ème , avec un calcul de racine.
en divisant par
déja visuellement, en remplaçant le
Ensuite, au lieu de se décerveler sous Excel,:bad:
l'idée est la suivante: on manie les encadrements à la main.
un point fixe , en règle générale, est limite de la suite récurrente
où la valeur initale
(cf. Dieudonné, "calcul infinitésimal" chez Hermann éditeur)
En fait , dans un intervalle I, où la fonction dérivée f'
est petite en valeur absolue.
alors
d'après l'inégalité des accroissements finis.
si
et
sur l'intervalle ouvert
voilà comment on peut procéder:
le diamètre de l'intervalle est passé de
et on itère.
on fait manier les inégalités à la main par les kids,
les valeurs approchées sont calculées en posant les divisions
euclidiennes. :marteau:
Il se trouve aussi que:
- les différentes valeurs d'encadrement trouvées correspondent
aux fractions continues obtenues visuellement,tronquées du
le plus imbriqué
en effet, "tout le monde" (
- les numérateurs et/ou dénominateurs ont à voir avec la suite
de Fibonacci
remarque: on sait que cette suite de Fibonacci
a pour équation caractéristique
Salut,
le serveur ne marche pas et je ne peux pas voir l'enonce du devoir.
Mais busard_des_roseaux, tu utilises un langage qui n'est pas adapte a un 3eme: en 3eme, on ne connait pas les fractions continues, ni les derivees, ni les suites...
Si je prend une phrase comme
le serveur ne marche pas et je ne peux pas voir l'enonce du devoir.
Mais busard_des_roseaux, tu utilises un langage qui n'est pas adapte a un 3eme: en 3eme, on ne connait pas les fractions continues, ni les derivees, ni les suites...
Si je prend une phrase comme
, je ne suis meme pas sur qu'un eleve de Terminale puisse comprendre.l'application f est contractante,la suite récurrente converge vers l'unique point fixe de l'intervalle.
ok, donc d'ici ça marche 
Pour la première question, on te demande tout simplement une valeur approchée grâce à la calculatrice.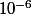 , ça veut dire avec 6 chiffres après la virgule.
, ça veut dire avec 6 chiffres après la virgule.
Mais attention, ça ne veut pas dire de garder tout simplement les 6 premiers chiffres.
Par exemple, pour 1,23456789, la valeur approchée est 1,234568 (parce que le chiffres suivant est supérieur à 5)
Pour la première question, on te demande tout simplement une valeur approchée grâce à la calculatrice.
Mais attention, ça ne veut pas dire de garder tout simplement les 6 premiers chiffres.
Par exemple, pour 1,23456789, la valeur approchée est 1,234568 (parce que le chiffres suivant est supérieur à 5)
bonsoir,
on considère la fonction

cette fonction associe à un nombre x son inverse augmenté de 1
sous Excel, il sufit de rentrer
$A2$=1+1/$A1$
et de faire l'expansion de cette formule avec la souris.
F2 est l'image de F1,F3 l'image de F2,etc..
normalement, dans ces cellules, on devrait obtenir des valeurs
de plus en plus approchées de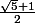
on considère la fonction
cette fonction associe à un nombre x son inverse augmenté de 1
sous Excel, il sufit de rentrer
$A2$=1+1/$A1$
et de faire l'expansion de cette formule avec la souris.
F2 est l'image de F1,F3 l'image de F2,etc..
normalement, dans ces cellules, on devrait obtenir des valeurs
de plus en plus approchées de
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
