Problème tangence de courbes

[doudou46]

bonjour à tous,
j'ai un problème avec la dernière question de mon DM...si quelqu'un pouvait me venir en aide, ce serait très gentil de votre part...
voilà, il s'agit de justifier le fait que deux courbes ln(x) et x^(1/e) sont tangentes. je pensais essayer de trouver le point intersection de ces deux courbes et montrer que la pente de la tangente est la même (= même dérivée) pour chacune des courbes.
mais je n'arrive pas à résoudre l'équation ln(x)=x^(1/e)... :briques:
merci d'avance et bonne fin de journé!

[Maks]

Bonjour. Je pense que ton énoncé est faux.

[Maks]

La démarche me paraît correcte. Il faut d'abord chercher le point d'intersection, puis évaluer les pentes des tangentes en ce point (elles doivent être identiques, comme tu l'as dit).

[Maks]

Et si tu posais, . En effet, je n'arrive pas à résoudre . Mais je pense que l'on peut s'intéresser à l'équation , puis voir si les solutions trouvées conviennent. Qu'en penses-tu ?

[Maks]

Euh, je viens de penser à un truc. Tu dis que cette question est la dernière de ton DM ... TU es sûr que ton DM n'a AUCUN rapport avec cette question, justement ? :marteau: Cela m'étonnerait fortement ...

[Maks]

Ah si, ma méthode marche ... C'est sympa ça !

[busard_des_roseaux]

bonjour,


je n'ai pas trouvé de solution au systeme



sauf erreur

:hum:

[Maks]

Moi si. J'ai d'abord résolu . Cette équation admet une unique solution. Il s'avère que cette solution est aussi solution de l'équation .

[Ericovitchi]

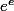
oui bien vu, c'est vrai que marche

[Maks]

Oui. :ptdr: