Nombre premiers entre eux - 3ème

[Jak-Okay]

Bonjour , je ne comprends pas très bien le sens d'une questions de mon dm ...

Voici l'énoncé :

n et p sont 2 nombres premiers entre eux . le nombre 2n et 4p sont-ils toujours premiers entre eux ? même question avec 3n et 5p ?

PS : je sais ce que c'est un nombre premiers mais ça m'aide pas beaucoup ...

merci de votre aide

[oscar]

Bonjour
2n et 4p soint divisibles par 2 si n et p € N donc ils ne sont PAS 1ers entre eux
Il n' est est pas de m^de 3n et 5p

[Maks]

Bonjour.
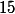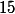Pour savoir si deux nombres sont premiers entre eux, tu peux t'intéresser à leurs diviseurs communs. Par exemple, et ne sont pas premiers entre eux car est un diviseur de et un diviseur de . Comme tu dois le savoir, deux nombres sont premiers entre eux si et seulement si leur unique diviseur commun est .
La question à se poser est alors : quels sont les diviseurs de ? Et ceux de 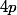? est-il le seul diviseur commun de et de 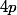? Conclusion.

[Maks]

Mais bon sang Oscar ! Arrête de donner les réponses toutes faites ! Laisse un peu chercher !

[camilie]

Bonjour,

Je pense que la question veut dire que si par exemple tu remplaces n ou p par un nombre ( et que par exemple tu fais: 2x2 et 4x2 ) si le résultat est un nombre premier.

[Maks]

Non Camilie. Tu confonds nombres premiers et nombres premiers entre eux. Revoie tes définitions.

[Jak-Okay]

Ok Maks , merci

Non je pense qu'ils ne sont pas premier entre eux car :
2n/2 , 4p/4 donc on peut simplifier

[Maks]

Pour le dire proprement, dis que les diviseurs de sont ... Que ceux de sont ... Et donc que ...

Et pour et alors ?

[Jak-Okay]

les diviseurs de 2n sont 1 et 2n , de 4p sont 1 et 4p donc ils sont premiers entre eux et avec 3n ils sont 1 et 3n et 5p ils sont 1 et 5p donc ils sont premiers entre eux

[Maks]

n'est-il pas diviseur de ? et de alors ?

Au passage, n est diviseur de , tout comme est diviseur de ! :marteau:

[Jak-Okay]

Ah oui effectivement alors 2n et 4p ne sont pas premiers entre eux

et pour 3n et 5p , là il n'y aucun diviseurs qui n'est pas 3 ou 1 donc ces deux nombres sont premiers entre eux

j'espère que j'ai bon , merci

[Maks]

Oui, tu as bon. Mais juste pour vérifier, donne moi la liste des diviseurs de , de , de , et enfin celle de (j'attends 4 listes).

Et alors, et sont-ils premiers entre eux ? (cette question n'a aucun rapport avec ce que je t'ai demandé juste au-dessus)

[Jak-Okay]

Ok mais pourquoi la liste ? ba je te l'avais donné au dessus enfaite
Je sais pas si c'est ça que tu veux :
2n : 1 , 2 , 3 , 4 , 6 , 8 , 10 , 12 ... ( nombre pairs )
4p : 1 , 2 , 4 , 6 , 8 ...
3n : 1 , 3 , 6 , 9 , 12 , 15 ...
5p : 1 , 5 , 10 , 15 ..

Non , ils ne sont pas premiers entre eux car 10/2 = 5

[Maks]

Non, tu n'as pas compris ce que je voulais.

Tu prends n et p deux nombres premiers fixés.
Je te demande alors la liste des diviseurs de , puis celle des diviseurs de , de , et enfin celle de .

[Jak-Okay]

désolé je vois pas trop ce que tu veux

2n : 1 et 2n
4p : 4 et 4p
3n : 3 et 3n
5p : 5 et 5p

mais je pense pas ce que c'est ça que tu attends :briques:

[Maks]

Je suis désolé, mais les diviseurs de sont , , et , si est premier (on pourrait même rajouter, en étant tatillon, , , 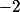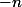et ). Tu comprends ce que je voulais ? Je voulais te faire remarquer que les diviseurs de ne sont pas QUE et ! Je ne veux pas te traumatiser avec les diviseurs, loin de là, je veux juste que tu comprennes bien, il n'y a là vraiment rien de compliqué.

Dis-moi si tu ne comprends pas.

[Jak-Okay]

Oui j'ai compris avec ton exemple

donc pour 4p ça serait : 1 , 2 , p , 4p
3n : 1 , n , 3n
5p : 1 , p , 5p

Autrement merci de ton aide , bonne journée

[Maks]

Non. Tu en as oublié pour et .

[Jak-Okay]

3n : 1 , n , 3n , 3

5p : 1 , p , 5p , 5

[Maks]

Voilà ! Bon, ça va, maintenant, tu as bien compris ?

Alors, maintenant, on vérifie sur un exemple (promis, après, j'arrête de t'embêter ! :ptdr: ) :

12 et 17 sont-ils premiers entre-eux ? (évidemment, tu dois justifier, comme je te l'ai expliqué).