Transformations complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sou71
- Membre Relatif
- Messages: 430
- Enregistré le: 05 Nov 2008, 17:51
-
 par sou71 » 15 Mai 2009, 20:41
par sou71 » 15 Mai 2009, 20:41
bonsoir, quelles propriétés peut ont appliquer sur:
^2)
je sais que
^2)
=

avec T =

mais existe il d'autres propriétés ? merci d'avance
-
matteo182
- Membre Relatif
- Messages: 279
- Enregistré le: 01 Mai 2005, 01:14
-
 par matteo182 » 15 Mai 2009, 21:06
par matteo182 » 15 Mai 2009, 21:06
Salut,
Hum à part remplacer
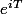
par
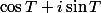
je vois pas trop quoi appliquer d'autre, et puis cela dépend peut-être aussi de pourquoi tu cherches des transformations.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 15 Mai 2009, 22:55
par Timothé Lefebvre » 15 Mai 2009, 22:55
Salut,
c'est la formule de De Moivre, elle dit que
^n=cos(n\theta)+isin(n\theta))
,
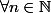
.
Il y a aussi celle que tu as donné.
Essaye avec ça.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 15 Mai 2009, 22:59
par uztop » 15 Mai 2009, 22:59
sou71 a écrit:je sais que
^2)
=

avec T =

Salut,
attention, il y a un peu trop d'étages dans ton exponentielle !
La formule juste est
^2 = e^{2i\theta})
, ce qui correspond à la formule de De Moivre que t'as donné Timothé
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 15 Mai 2009, 23:02
par Timothé Lefebvre » 15 Mai 2009, 23:02
On peut aussi l'appliquer pour tout n naturel

Tel que

ce qui est très logique en fait.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 15 Mai 2009, 23:04
par uztop » 15 Mai 2009, 23:04
oui tout à fait, quand on l'écrit de cette façon, la formule de De Moivre est toute simple !
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 15 Mai 2009, 23:13
par Timothé Lefebvre » 15 Mai 2009, 23:13
D'ailleurs on peut appliquer le Binôme de Newton au calcul de
)
et
)
en fonction de
)
et
)
, sympa à faire.
-
sou71
- Membre Relatif
- Messages: 430
- Enregistré le: 05 Nov 2008, 17:51
-
 par sou71 » 16 Mai 2009, 15:13
par sou71 » 16 Mai 2009, 15:13
oui, merci beaucoup, j'ai réussi ce que j'avais à faire
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités