Problèmes de math devoir noté

[patmol02]

Bonjour tout le monde!

J'ai deux problèmes de math à faire pour lundi. Cependant, après de longues heures de réflexion, je ne vois pas du tout comment les résoudre! Il serait important pour moi de réussir, car j'ai vraiment besoin d'une bonne note :we: !

Voici les deux problèmes :

1er :

Dans l'hypermonde, les mondes sont numérotés 1,2,3,... Le grand mage possède la faculté de se mouvoir dans les deux sens entre n'importe quels mondes n et 2n, ainsi que n et 3n+1.
En partant d'un monde quelconque, le grand mage est-il capable de visiter n'importe quel autre monde?

2eme:

Soit P(x) un polynôme de degré 6, tel que, pour deux nombres réels a et b,
P(a) = P(-a) et P(b) = P(-b) et en outre P'(0) = 0.
Prouver que pour tout nombre réel x, P(x) = P(-x).


Alors voila, si qqn sait les résoudre, je suis tout ouvert à écouter ses explications! Je vous remercie d'avance, et vous souhaite une belle journée!

[Sa Majesté]

Bonjour tout le monde!

J'ai deux problèmes de math à faire pour lundi. Cependant, après de longues heures de réflexion, je ne vois pas du tout comment les résoudre! Il serait important pour moi de réussir, car j'ai vraiment besoin d'une bonne note :we: !

Voici les deux problèmes :

1er :

Dans l'hypermonde, les mondes sont numérotés 1,2,3,... Le grand mage possède la faculté de se mouvoir dans les deux sens entre n'importe quels mondes n et 2n, ainsi que n et 3n+1.
En partant d'un monde quelconque, le grand mage est-il capable de visiter n'importe quel autre monde?

2eme:

Soit P(x) un polynôme de degré 6, tel que, pour deux nombres réels a et b,
P(a) = P(-a) et P(b) = P(-b) et en outre P'(0) = 0.
Prouver que pour tout nombre réel x, P(x) = P(-x).


Alors voila, si qqn sait les résoudre, je suis tout ouvert à écouter ses explications! Je vous remercie d'avance, et vous souhaite une belle journée!

Salut

D'après toi quelles sont les conditions sur les coefficients du polynôme pour que P(x) = P(-x) pour tout x réel ?

Que donne P'(0) = 0 ?

[patmol02]

Comme condition initiale, on nous donne deux nombres réels pour lesquels la fonction est paire, ainsi qu'une info sur sa dérivée en x= 0. Et d'après ce que j'ai compris, on cherche à prouver que cette fonction est paire
(P(x) = P (-x)). Est-ce juste? Sinon je vois pas du tout comment commencer la démo :triste:

[patmol02]

ya pas qqn qui a une explication ou une soluce svp? :cry:

[Ericovitchi]

Ecris un polynome du 6 ième degré et traduis ce que l'on te dis.
Par exemple on trouve facilement que f'(0)=0 veut dire que le polynôme n'a pas de terme en x
Traduis f(-a) = f(a) et f(-b)=f(b) et essayes d'en déduire que ton polynome n'a pas non plus de terme en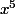 , ni en et qu'il n'a donc que des termes pairs.

[patmol02]

merci de la réponse, mais j'ai un peu de mal a comprendre :triste:

Je ne comprend pas pourquoi un polynôme n'a pas de terme en x lorsque que sa dérivée en x = 0 est nulle. Sinon, je vois à peu près ou tu veut en venir quand tu dis qu'il n'y a pas de x^5 et de x^3, mais j'ai aucune idée de comment tu peut l'affirmer (grace a quelle condition).

merci du temps que vous passez a m'aider! :we:

[Ericovitchi]

Par exemple pour f'(0)=0, il suffit de prendre un polynôme quelconque :

de le dériver :


de faire x=0 et on trouve f'(0)=f=0 donc le polynôme n'a pas de terme en x

Fais pareil avec les autres conditions et tu trouveras qu'il n'y a pas non plus de termes en et en

[patmol02]

Ah d'accord! Je vois ou tu veux en venir, merci! J'ai compris ta démarche pour P'(0) = 0, par contre, je ne vois pas trop comment me servir des deux autres conditions ( P(-a) = P(a) et P(-b) = P(b) ) pour me débarrasser de x^5 et x^3. Une explication?

Et donc si j'ai bien compris, le but est de supprimer les termes impaires, tout cela dans le but d'affirmer la parité de la fonction ( P(-x) = P(x) ). C'est juste?

[Ericovitchi]

Tu dis à chaque fois que tu ne vois pas mais tu as essayé au moins de faire P(-a)=P(a) dans le polynôme du 6 ième degré ?

[patmol02]

(Pardon pour le message privé, j'avais pas vu immédiatememnt que tu avait deja repondu) Oui oui, j'ai remplacé x dans mon polynome (zx^6 + yx^5 + wx^4 + vx^3 + ux^2 + sx + r) par -a, que j'égal au même polynôme auquel j'avais remplacé x par a (d'ou P(-a) = P(a) ).

J'ai donc za^6 - ya^5 + wa^4 - va^3 + ua^2 - sa + r
=
za^6 - ya^5 + wa^4 - va^3 + ua^2 - sa + r

pis après en simplifiant, je vois pas comment prouver qu'il n'y a pas de x^5 et de x^3 dans ce polynome... erf quoi :triste:

[Ericovitchi]

C'est pas tout à fait ça :


Tu sais deux autres choses : d'abord s=0 et puis cette équation est aussi vraie pour un autre point, le point b.

Deux équations, deux inconnues (y et v) :id:

[patmol02]

Donc si je comprend bien,

za^6 - ya^5 + wa^4 - va^3 + ua^2 - 0 + r
=
za^6 + ya^5 + wa^4 + va^3 + ua^2 + 0 + r

et

zb^6 - yb^5 + wb^4 - vb^3 + ub^2 - 0 + r
=
zb^6 + yb^5 + wb^4 + vb^3 + ub^2 + 0 + r

(Ces deux équations sous formes de système).
Donc je dois résoudre le système d'équation suivant :

2ya^5 + 2va^3 = 0 --> v = -ya^2
2yb^5 + 2vb^3 = 0

--> 2*y*b^5 - 2*y*a^5*b^3 = 0 (ici je met des * pour une meilleure compréhension), ce qui me donne un truc du genre b^5 = a^5*b^3

Mais la, je sais pas trop comment interprété cette solution et surtout comment continuer.

[Ericovitchi]

Voyons tu as un système



Les a et b sont des constantes et les inconnues sont les y et v.
Tu peux résoudre ça comme tu veux, mais à moins que le système soit indéterminé (ce qui arrive si a=b mais on va admettre que les points étaient distincts) la seule solution c'est y=0 et v=0

[patmol02]

ah d'accord, donc vu que y = 0 (coefficient du terme x^5) et v = 0 (coefficient du terme x^3), alors le polynome est exprimé sous la forme zx^6 + wx^4 + ux^2 + r ? Il est donc bien pair parce que dans ce cas P(x) est bien égal à P(-x). CQFD

Elle est juste ma fin de démo?

En tout cas un grand merci a toi pour m'avoir aider

[Ericovitchi]

Oui voilà tu as tout trouvé.

[patmol02]

yeah cool, merci encore, par contre tu n'a pas une idée de comment commencer pour l'autre problème, parce que j'ai déjà un pu de mal au niveau de la compréhension (j'ai du mal a me représenter le passage d'un monde n à 2n ou 3n+1). Une idée?

[Ericovitchi]

Cherches un peu.
Vois le passage comme une fonction qui fait correspondre un nombre à un autre nombre et regardes si tout nombre est atteint.
(l'astuce est dans les mots "dans les deux sens")

[patmol02]

Piou, pour celui la je vois vraiment pas... je pige pas cette histoire de deux sens. Si admettons il est dans le monde 6 et qu'il veut revenir dans un monde précédent grace au passage 2n, il va retomber sur quoi 3? Par contre pour 3n+1 je vois pas comment ca marche!

Comment pourrais-je lié ces deux notions... aucune idée, je chercher pendant 1 heure avant, pas moyen...

Mon dieu... les math... xD

[patmol02]

Erf, personne à une idée?

je remet le porblème que je dois résoudre ici :

Dans l'hypermonde, les mondes sont numérotés 1,2,3,... Le grand mage possède la faculté de se mouvoir dans les deux sens entre n'importe quels mondes n et 2n, ainsi que n et 3n+1.
En partant d'un monde quelconque, le grand mage est-il capable de visiter n'importe quel autre monde?


Svp, ce serait super si qqn arrivait à m'expliquer comment le résoudre. Merci d'avance!

[Ericovitchi]

il faut que tu regardes s'il peut aller d'un nombre p à un nombre q en utilisant juste les deux fonctions 2n et 3n+1.

Comme il peut aller dans les deux sens, on peut supposer que q>p sans dénaturer le problème.
On peut essayer de regarder où on peut aller depuis le monde 1 car si on sait aller de 1 à p et de 1 à q alors on saura aller de p à q.

Donc le problème revient à regarder si en partant de 1 et en générant les nombres 2n (donc 2, 4, 8,16, ...) et 3n+1 (1,5,7,10 ...) on sait atteindre tous les nombres.
On voit très vite que non car par exemple depuis 1 on atteint pas 3