dans un recipient de forme cylindrique de rayon 4 cm ,on place une bille de rayon 2cm.
on verse ensuite de l'eau jusqu'a recouvrir exactement la bille:la surface du liquide est tangente a la bille.
on retire alors la bille ,et on la remplace par une autre bille dont le rayon R n'est pas egal a 2cm.
est-il possible d'obtenir de nouveau la meme situation ,c'est-a-dire que la surface de l'eau soit encore tangent a la bille?
1° calculer le volume d'eau versé dans le recipient.
( j'ai trouvé 160pi/3)
2° a)si l'on veut que la nouvelle bille puisse entrer dans le recipient,a quel intervalle appartient le rayon R?
j'ai trouvé ]0;4[
b)en calculant de deux façons le volume "bille +eau" montrer qu'une bille est solution du probleme posé si son rayon R verifie l'equation:
R(au cube)-24R+40=0
verifier que 2 est solution.pouvaiton le prevoir?
celle-la je n'arrive pas
3°a l'ecran d'une calculatrice,visualiser la courbe d'equation:
y=x(au cube)-24x+40
justifier graphiquement qu'il existe une bille de rayon R autre que 2,solution du probleme posé.
donner une valeur approchée a O,1 prés de son rayon.
j'ai trouvé 3,6
POUR ALLER PLUS LOIN
1°verifier que x(au cube)-24x+40 s'ecrit (x-2)(X²+2x-20) et que x²+2x-20=(x+1)²-21.
il suffit de develloper ceux qui sont entre parenthese
2°determiner algebriquement le rayon exact R de la bille.
je comprend pas la consigne
est-ce que qqn peut me faire la 2°b) et la derniere ?svp
je risque de ne pas pouvoir vous repondre car je suis a l'internat.
DM avec equation
4 messages
- Page 1 sur 1
Salut et bienvenue à toi.
Tout d'abord, pourrais tu essayer d'expliquer comment tu trouves les différents résultats.
Question 2.b :
Tu supposes simplement que le rayon de la boule est R, et tu fais le même raisonnement que la question 1.
Dernière question :
Déterminer "algébriquement" : tu peux comprendre ce mot comme "de manière exacte".
Tu as montré à la question 3, que la valeur était environ 3,6. Maintenant on te demande la valeur exacte. N'hésite surtout pas à utiliser les questions précédentes.
Tout d'abord, pourrais tu essayer d'expliquer comment tu trouves les différents résultats.
Question 2.b :
Tu supposes simplement que le rayon de la boule est R, et tu fais le même raisonnement que la question 1.
Dernière question :
Déterminer "algébriquement" : tu peux comprendre ce mot comme "de manière exacte".
Tu as montré à la question 3, que la valeur était environ 3,6. Maintenant on te demande la valeur exacte. N'hésite surtout pas à utiliser les questions précédentes.
déterminer algébriquement ça veut dire quoi ?
Ca veut dire résoudre l'équation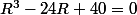
et comme tu connais déjà une racine (2) il te suffit de résoudre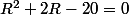
On t'a donné une indication puisque tu sais que ça peut être mis sous la forme^2-21=0)
(attention c'est bien R+1, il semble y avoir une erreur dans ton énoncé)
Un petit effort maintenant. Ne reconnais tu pas une identité remarquable ?
Ca veut dire résoudre l'équation
et comme tu connais déjà une racine (2) il te suffit de résoudre
On t'a donné une indication puisque tu sais que ça peut être mis sous la forme
(attention c'est bien R+1, il semble y avoir une erreur dans ton énoncé)
Un petit effort maintenant. Ne reconnais tu pas une identité remarquable ?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
