Tangentes perpendiculaires entre elles...
17 messages
- Page 1 sur 1
tangentes perpendiculaires entre elles...
Bonjour!
Je coince sur cet exercice :
Soit f la fonction définie sur R par : f(x)= -x²+5x-4 et P sa représentation dans un repère orthonormal.
[B]Déterminer l'ensemble des points qui appartiennent à deux tangentes à P, perpendiculaires entre elles.
Merci!
Je coince sur cet exercice :
Soit f la fonction définie sur R par : f(x)= -x²+5x-4 et P sa représentation dans un repère orthonormal.
[B]Déterminer l'ensemble des points qui appartiennent à deux tangentes à P, perpendiculaires entre elles.
Merci!
Oui, j'avais deux trois pistes, mais je n'arrive pas à en tirer des réponses.
Par exemple, j'ai penser à prendre deux tangentes Ta et Tb dc les équations sont Ta : y=(-2a+5)x+a²-4 et Tb pareil, avec b a la place de a
et donc, je me suis dis : deux droites sont perpendiculaires ssi le produit de leur coef dir est égal à -1
Et donc (-2a+5)(-ab+5) = -1
Bla bla je trouve a=26/6b
et ça m'arrange pas franchement d'exprimer a en fonctionde b...
Par exemple, j'ai penser à prendre deux tangentes Ta et Tb dc les équations sont Ta : y=(-2a+5)x+a²-4 et Tb pareil, avec b a la place de a
et donc, je me suis dis : deux droites sont perpendiculaires ssi le produit de leur coef dir est égal à -1
Et donc (-2a+5)(-ab+5) = -1
Bla bla je trouve a=26/6b
et ça m'arrange pas franchement d'exprimer a en fonctionde b...
Tu as déjà trouvé pas mal de choses.
Récapitulons :
Une tangente a pour équation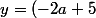x+a^2-4) correct
correct
Donc un point (x,y) qui appartient à deux tangentes satisfait le système
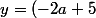x+a^2-4)
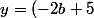x+b^2-4)
Et en plus elles doivent être perpendiculaires donc (-2a+5)(-2b+5)=-1
Ca n'est pas très difficile à résoudre. Résous le premier système en trouvant x et y (ça donne x=(a+b)/2, y= ....
puis à l'aide de la seconde relation (remplaces les ab par les a+b et poses a+b = t pour respecter la symétrie du problème) tu devrais trouver x et y fonction d'un seul paramètre (t) ce qui te donnera en fait les équations paramétriques de la courbe recherchée et si tu élimines le paramètre, tu trouveras la courbe.
PS. c'est une propriété connue de la parabole, tu dois trouver une droite parallèle à l'axe des x
Récapitulons :
Une tangente a pour équation
Donc un point (x,y) qui appartient à deux tangentes satisfait le système
Et en plus elles doivent être perpendiculaires donc (-2a+5)(-2b+5)=-1
Ca n'est pas très difficile à résoudre. Résous le premier système en trouvant x et y (ça donne x=(a+b)/2, y= ....
puis à l'aide de la seconde relation (remplaces les ab par les a+b et poses a+b = t pour respecter la symétrie du problème) tu devrais trouver x et y fonction d'un seul paramètre (t) ce qui te donnera en fait les équations paramétriques de la courbe recherchée et si tu élimines le paramètre, tu trouveras la courbe.
PS. c'est une propriété connue de la parabole, tu dois trouver une droite parallèle à l'axe des x
Déjà x+a^2-4=(-2b+5)x+b^2-4) est facile à résoudre. Il faut mettre tous les x d'un coté
est facile à résoudre. Il faut mettre tous les x d'un coté
=b^2-a^2) et en se souvenant que
et en se souvenant que (b+a)) il y a un (b-a) qui se simplifie
il y a un (b-a) qui se simplifie
et ça donne
Ensuite tu remplaces x par (a+b)/2 dans l'une des deux expressions et tu simplifies. Ca donne/2 - ab - 4)
Ensuite en exploitant (-2a+5)(-2b+5)=-1 il faut que tu arrives à te débarrasser des a et b en créant une seule équation en x,y
Ça n'est pas difficile. respectes bien la symétrie des expressions en a et b.
et ça donne
Ensuite tu remplaces x par (a+b)/2 dans l'une des deux expressions et tu simplifies. Ca donne
Ensuite en exploitant (-2a+5)(-2b+5)=-1 il faut que tu arrives à te débarrasser des a et b en créant une seule équation en x,y
Ça n'est pas difficile. respectes bien la symétrie des expressions en a et b.
Wouha! Merci Ericovitchi !
Après quelques heures de calcul ( à cause d'une erreur qui s'était glissée dans un paramètre) je suis arrivé à un résultat plausible.
J'aime ce principe, qui consiste à nous guider, mais pas nous mâcher le travail... On a plus l'impression de remporter une petite victoire !
Merci de ne pas m'avoir laissé tomber.
Après quelques heures de calcul ( à cause d'une erreur qui s'était glissée dans un paramètre) je suis arrivé à un résultat plausible.
J'aime ce principe, qui consiste à nous guider, mais pas nous mâcher le travail... On a plus l'impression de remporter une petite victoire !
Merci de ne pas m'avoir laissé tomber.
Sos
J'ai le même exercice que toi grand charles à faire, et je n'arrive pas à résoudre: (-2a+5) (-2b+5) = -1 :hein:
Si tu pouvais m'expliquer comment tu as fait, ce serait gentil, merci
Si tu pouvais m'expliquer comment tu as fait, ce serait gentil, merci
Merci pour ton aide
Donc si j'ai bien compris l'ensemble des points qui appartiennent à deux tangentes à P, perpendiculaires entre elles, est la droite d'équation y= 5/2
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

