Suite qui converge vers e

[lyceen09]

Bonjour!
Je viens ici pour vous demandez un peu d'aide sur la dernière question de mon DM sur laquelle je bute depuis plusieurs jours... Je replace la question dans son contexte, on cherche l'irrationalité de e.

Tout d'abord j'ai démontrer que pour tout n de IN* de k=0 à n et sont adjacentes et on pose leur limite commune. Ensuite j'ai bien démontrer que cette limite est irrationelle

Puis, on introduit pour tout n de IN et j'ai prouvé que

Et c'est la que sa se complique ^^ :

Je dois exprimer pour tout n de IN*, en fonction de





Je dois alors calculer alors la limite , mais là.. :/

[lyceen09]

Pour simplifier ma demande :

Quelqu'un voit comment je pourrais calculer cette limite :



Une intégration par parties ramènent au point de départ..

[lyceen09]

Réglé : série telescopique :we:

[Ericovitchi]

Une piste : En intégrant par partie en prenant et
ça donne Donc

[Ericovitchi]

A mon avis il faut remettre les sigma dans les intégrales et utiliser le fait que
multiplié par ca va se simplifier et s'intégrer très bien
Mais est peut-être justement ce qu'on veut démontrer donc je ne sais pas si on a vraiment le droit d'utiliser ça.

[Cheche]

Salut,

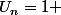
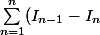Remarque : Dans ta somme, tu n'as pas plein de terme qui se simplifie deux à deux.

(I0-I1) + (I1-I2) + (I2-I3) + (I3-I4) + ...