Triples Intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chacalpuant
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Avr 2009, 13:36
-
 par chacalpuant » 02 Mai 2009, 17:27
par chacalpuant » 02 Mai 2009, 17:27
Bonjour,
Voici le sujet de l'exercice :
Find the volume of the region bounded above by the paraboloid z=9-x^2-y^2, below by the xy-plane, and lying outside the cylinder x^2+y^2=1.
Merci de votre aide
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 02 Mai 2009, 17:33
par Euler07 » 02 Mai 2009, 17:33
Hello,
We don't (I think) speak English here !
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 02 Mai 2009, 17:35
par Euler07 » 02 Mai 2009, 17:35
Bon tu as au début
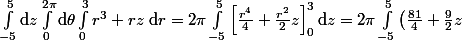 \mathrm{d}z = 2 \pi \left[ \frac{81}{4}z + \frac{9}{4}z^2 \right]^5_{-5} = .......)
-
chacalpuant
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Avr 2009, 13:36
-
 par chacalpuant » 02 Mai 2009, 17:49
par chacalpuant » 02 Mai 2009, 17:49
Merci, tu peux m'expliquer comment tu fais ?
PS : Trouver le volume de la région délimitée ci-dessus par le paraboloïde z = 9-x ^ 2-y ^ 2, et située à l'extérieur du cylindre x ^ 2 + y ^ 2 = 1.
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 02 Mai 2009, 17:55
par Euler07 » 02 Mai 2009, 17:55
C'est facile tu commence avec la définition de ton cour :
 dx d y d z= {\displa... ...splaystyle\int_{\alpha(x,y)}^{\beta(x,y)}} f(x,y,z) d z\right) dy\right) dx $)
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 02 Mai 2009, 18:01
par Euler07 » 02 Mai 2009, 18:01
Tu te sert de ton cour !
\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = \int_{z_1}^{z_2}\!\int_{y_1(z)}^{y_2(z)}\!\int_{x_1(z,y)}^{x_2(z,y)}f(x,y,z)\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z)
-
chacalpuant
- Membre Naturel
- Messages: 21
- Enregistré le: 26 Avr 2009, 13:36
-
 par chacalpuant » 02 Mai 2009, 18:37
par chacalpuant » 02 Mai 2009, 18:37
comment tu trouve les variables x2, y2 ... ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 03 Mai 2009, 21:19
par Pythales » 03 Mai 2009, 21:19
Moi j'aurais dit
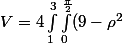\rho d\rho d\theta)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 03 Mai 2009, 21:25
par Pythales » 03 Mai 2009, 21:25
Moi j'aurais dit
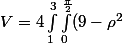\rho d\rho d\theta)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
