Suite et intégrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sossounette
- Membre Naturel
- Messages: 43
- Enregistré le: 30 Oct 2006, 17:53
-
 par Sossounette » 28 Avr 2009, 19:19
par Sossounette » 28 Avr 2009, 19:19
Bonsoir,
J'essaie de faire un exercice mais je n'arrive pas à le faire.
In =
) dx)
J'ai réussi a démontrer que 1/(x(1+x^n)) < 1/x et que In < ln(2)
Je dois maintenant démontrer que In est croissante, mais je ne vois pas comment faire. Dois-je utiliser la récurrence en faisant l'hypothèque que I(n+1)=I(n) ? Mais si c'est cela comment dois-je faire. Est ce que c'est bon si je multiplie des deux cotés par (1+x^n)
Merci pour vos réponses
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 28 Avr 2009, 19:31
par Joker62 » 28 Avr 2009, 19:31
Haileau
Pour montrer que I_n est croissante, tu étudies le signes de I_(n+1) - I_n
-
Sossounette
- Membre Naturel
- Messages: 43
- Enregistré le: 30 Oct 2006, 17:53
-
 par Sossounette » 28 Avr 2009, 23:20
par Sossounette » 28 Avr 2009, 23:20
In+1 - In =
 dx - \int_{1/2}^{1} 1/(x(1+x^(n+1)) dx)
 - 1/(x(1+x^(n+1)) dx)
) - x(1+x^n)] / x(1+x^n) * x(1+x^(n+1)) dx)
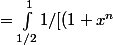*(1+x^(n+1))] dx)
Est ce que cela est correcte, s'il vous plait.
Merci de m'aider
-
JPzarb
- Membre Naturel
- Messages: 81
- Enregistré le: 21 Avr 2009, 13:37
-
 par JPzarb » 28 Avr 2009, 23:29
par JPzarb » 28 Avr 2009, 23:29
Salut,
Je me trompe peut être, mais tu devrais revoir la siplification du numérateur entre les lignes 3 et 4,
J'ai au numérateur : x(x^(n+1) - x^n)
ou encore x^(n+1) (x-1)
Du coup je comprends pas trop comment tu simplifie avec le x² du dénominateur ??
A bientot
ps : c'est In-In+1 (et non l'inverse)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités
