Intégrale avec changement de variable

par **Okinawa** » 27 Avr 2009, 20:52

Bonjour, j'ai une intégrale à calculer mais j'ai du mal, je sais plus où j'en suis entre tous les trucs à utiliser ... (formule du binome ... etc ...)
L'intégrale est :

intégrale de 0 à racine de 3 de : 1/((1+x²)^4) dx

En utilisant le changement de variable : x=tan t

(dsl si c'est pas très lisible)

Merci de votre aide !

par **Okinawa** » 27 Avr 2009, 21:12

Avec le changement de variable, j'arrive à :
Intégrale de 0 à pi/3 de : 1/(cos t)^6 dt
(ou cos t ^6 dt ... )

par **fatal_error** » 27 Avr 2009, 21:19

salut,

je suppose que c'est juste.
Est-ce qu'on peut pas dire que

Ca simplifierait bien les calculs

par **Ericovitchi** » 01 Mai 2009, 11:51

Moi je trouve plutôt

Après il suffit d'exprimer le

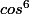
en fonction de cos(6x), cos4x, cos2x, ...

par **mathelot** » 01 Mai 2009, 13:33

Bonjour,

on a l'identité

l'intégrale devient

c'est une intégrale style Wallis.
soit on linéarise en posant

et formule du binôme, ou intégration par parties

par **Ericovitchi** » 01 Mai 2009, 14:18

oui mais le dx fait un

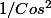
donc ça en enlève 2

par **mathelot** » 01 Mai 2009, 14:50

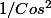
Ericovitchi a écrit:oui mais le dx fait un donc ça en enlève 2

8- 2 ? :doh:

par **Ericovitchi** » 01 Mai 2009, 14:56

ha oui OK. désolé

par **Okinawa** » 03 Mai 2009, 17:09

Merci bcp (et dsl pour le retard j'avais plus internet...)

Intégrale avec changement de variable

Intégrale avec changement de variable

Qui est en ligne