Question sur un exercice de DM

[Huppasacee]

2. Déterminer une équation cartésienne de la droite d’équation D1 perpendiculaire à D et passant par M et la tracer.

puis :

3. En déduire les coordonnées de H projeté orthogonal de M sur D puis calculer MH.

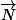
il a pu être déterminé de plus que pouvait avoir comme coordonnées :
(2 ; -1 ) car l'équation de D est 2x-y+1=0, soit : a = 2 et b = -1

[lasute]

A d'accord, et pour les question 1.a de la partie 2, la réponse que j'ai mise est elle bonne ?

[lasute]

Et pour la question 1.a:
On sait que D est la droite passant par A de vecteur normal n, M est un point quelconque du plan et H est son projeté orthogonal sur D.
D'où [AH] est perpendiculaire à [HM].
Donc H est le projeté orthogonal de A sur [HM].
On sait que H est le projeté orthogonal de A sur [HM].
D'où vAM.n=vHM.n

A d'accord, et pour la réponse que j'ai mise, est elle bonne ?

[lasute]

et pour la question 1.b de la partie 2 si je met :

Soit d la longueur HM
On sait que vAM.vn=vHM.vn
(Quand je met |HM| c'est norme de HM)
D'où |HM|=|vAM.vn|/|vn|
et donc d=|vAM.vn|/|vn|

et pour cette question je ne suis pas sur que se soit bon en mettant "Soit d la longueur HM" ???

[lasute]

Et pour la question 2.b je pensais mettre:
On sait que AM.n=ax+by+c
De plus, n(a;b) d'où |n|(norme de n)=racine de (a²+b²)
Or on sait que d=|AM.n|/|n|
Donc d=|ax+by+c|/racine de (a²+b²)

est ce que c'est bon ou pas?

[lasute]

Par contre pour la question c je ne vois trop ce que je dois faire, je ne vois pas ce que je dois obtenir???

[lasute]

Quelqu'un peut il m'aider???

[Corrigane]