bonjour,
j'ai un devoir maison a faire et je n'arrive meme pas a repondre a la premiere question. La voici :
etude de la suite (Un) définie sur N* par Un = (1 + 1/n)^n
une erreur serait de dire que "la suite est de la forme (a)^n avec a>1 et que par conséquent,elle a pour limite +l'infini.
1) montrer que la suite converge vers e.
je crois qu'il faut trouver la limite de Un en +l'infini sauf que quoi que je fasse je tombe sur 1...je vois pas comment trouver e.
merci de votre aide.
swann
Convergence d'une suite
13 messages
- Page 1 sur 1
non j'ai vraiment que ça au début..c'est la premiere question..
en dessous il y a juste marqué :
"savoir que la suite converge vers e est un renseignement interessant mais seulement qualitatif. nous allons essayer d'obenir des renseignements quantitatifs en encadrant les termes Un ou e-Un" mais ça se rapporte aux questions suivantes.
Je suis en terminale S spé maths, mais c'est un devoir d'obligatoire...elle a dit qu'il était assez dur.
ça me rassure de vous entendre dire que c'est balaise..je desperais là :(
je dois donc faire ln(Un) .?? mais vous pouvez m'expliquer pourquoi ?
en dessous il y a juste marqué :
"savoir que la suite converge vers e est un renseignement interessant mais seulement qualitatif. nous allons essayer d'obenir des renseignements quantitatifs en encadrant les termes Un ou e-Un" mais ça se rapporte aux questions suivantes.
Je suis en terminale S spé maths, mais c'est un devoir d'obligatoire...elle a dit qu'il était assez dur.
ça me rassure de vous entendre dire que c'est balaise..je desperais là :(
je dois donc faire ln(Un) .?? mais vous pouvez m'expliquer pourquoi ?
Pour tout entier naturel  non nul,
non nul, ^n\right]=n\times \ln\left(1+\frac{1}{n}\right)=\frac{1}{\frac{1}{n}} \times \ln\left(1+\frac{1}{n}\right)= \frac{\ln\left(1+\frac{1}{n}\right)}{\frac{1}{n}})
Or,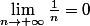 , on va donc utiliser le fait que la fonction ln soit dérivable en 1:
, on va donc utiliser le fait que la fonction ln soit dérivable en 1: }{x}=1) , avec
, avec 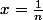 .
.
On obtient}{\frac{1}{n}}\right] =1) , donc
, donc ^n\right]=1) .
.
Comme la fonction exponentielle est continue sur R, on a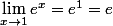 .
.
En remplaçant par
par ^n\right]) , on obtient
, on obtient \right]=e) .
.
Comme(n)=n) pour tout entier naturel
pour tout entier naturel  non nul, on en déduit que
non nul, on en déduit que ^n=e) .
.
voilà (il y a d'autres démo possibles, en voici une)
Or,
On obtient
Comme la fonction exponentielle est continue sur R, on a
En remplaçant
Comme
voilà (il y a d'autres démo possibles, en voici une)
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
