Les équations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 17 Avr 2009, 16:20
par Billball » 17 Avr 2009, 16:20
1 racine évidente donc ...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 17 Avr 2009, 16:21
par Timothé Lefebvre » 17 Avr 2009, 16:21
Tu es en seconde donc ?
Comme le dit Billball il y a bien une racine évidente qui devrait te sauter aux yeux !
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 16:32
par sophie57490 » 17 Avr 2009, 16:32
J'ai trouvé !
 = 1)
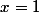
C'est ça ?
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 17 Avr 2009, 16:33
par Billball » 17 Avr 2009, 16:33
non, ca ca marche si c'est = 0 certainement pas 1
1 racine évidente je répéte
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 16:48
par sophie57490 » 17 Avr 2009, 16:48
Evidente, mais j'ai beau cherché, je ne la trouve pas ...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 17 Avr 2009, 16:49
par Timothé Lefebvre » 17 Avr 2009, 16:49
Je crois que tu n'as pas bien compris ce que Billball disait !
Il dit "1 racine évidente" : ça ne veut pas dire qu'il y a "une racine évidente" mais que 1 est une racine évidente !
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 17:01
par sophie57490 » 17 Avr 2009, 17:01
Faut tout mettre en racine carré ?
-
sb30
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Avr 2009, 16:16
-
 par sb30 » 17 Avr 2009, 17:05
par sb30 » 17 Avr 2009, 17:05
Le therme "racine" pour un polynôme signifie solution; ici si tu remplace x par 1 dans l'équation cela fait bien 0.
De cela on en déduit une factorisation et donc la deuxième "racine" ...
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 17:30
par sophie57490 » 17 Avr 2009, 17:30
Je comprends pas ...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 17 Avr 2009, 17:34
par Timothé Lefebvre » 17 Avr 2009, 17:34
Que ne comprends-tu pas ?
Ton équation a deux solutions, la première c'est 1.
Avec ça tu peux factoriser et trouver la deuxième !
-
sb30
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Avr 2009, 16:16
-
 par sb30 » 17 Avr 2009, 18:00
par sb30 » 17 Avr 2009, 18:00
si tu as un polynôme du second degrés du type x²-ax+b=0 alors tu peut le factoriser de la manière suivante : (x-x1)(x-x2) = 0 avec x1 et x2 les "racines" de l'équation
Avec ça et avec ce que l'on t'a donné comme info tu doit pouvoir y arriver.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 17 Avr 2009, 18:04
par Timothé Lefebvre » 17 Avr 2009, 18:04
Sauf que ça ne serait pas bon comme justification pour un devoir de seconde ...
-
sb30
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Avr 2009, 16:16
-
 par sb30 » 17 Avr 2009, 18:10
par sb30 » 17 Avr 2009, 18:10
Timothé Lefebvre a écrit:Sauf que ça ne serait pas bon comme justification pour un devoir de seconde ...
Effectivement :briques:, désolé.
En relisant la dernière question j'ai l'impression qu'il faut simplement s'assurer que les valeurs lus sur le graphique vérifie l'équation (pour valider que les solutions lus sont les bonnes).
Donc il n'est pas utile de chercher à résoudre par le calcul l'équation ??
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 17 Avr 2009, 18:12
par Timothé Lefebvre » 17 Avr 2009, 18:12
sb30 a écrit:Donc il n'est pas utile de chercher à résoudre par le calcul l'équation ??
Ca me semble effectivement dur en seconde !
L'interprétation graphique paraît être une bonne solution alternative pour trouver la réponse.
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 18:18
par sophie57490 » 17 Avr 2009, 18:18
Non, il faut faire par le calcul puisqu'il est demandé " Vérifier qu'il est bien ainsi par le calcul"
-
sb30
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Avr 2009, 16:16
-
 par sb30 » 17 Avr 2009, 18:25
par sb30 » 17 Avr 2009, 18:25
sophie57490 a écrit:Non, il faut faire par le calcul puisqu'il est demandé " Vérifier qu'il est bien ainsi par le calcul"
Oui on est d'accords cela signifie (c'est comme cela que je l'interprête), qu'il faut lire les solutions sur le graphique et ensuite remplacer x par ces valeur dans le polynôme et trouver que cela fait bien 0. On vérifie ainsi par le calcul que les solutions lus sont exactes.
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 18:32
par sophie57490 » 17 Avr 2009, 18:32
Ahh d'accord , effectivement ça donne le même résultat =D
-
sophie57490
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2006, 20:35
-
 par sophie57490 » 17 Avr 2009, 18:52
par sophie57490 » 17 Avr 2009, 18:52
Merci beaucoup de votre aide ..
A bientot
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
