Equation 2nd degré + limites

[chuchi]

bonjour,

j'ai 3 petits truc ou je blque sur des exos

I/ Soit
Calculer module et argument des solutions

Je trouve même pas les solutions...

II/

je devrais trouver un...

et

III/

forme indéterminé du type "0/0"...

merci !

[oscar]

Bjr

3) lim (e^cos x - e)/ x si x---> 0 forme 0/0

Règle de l' Hospital

=> lim (-sinx*e^cos x -1)/ 1=

[chuchi]

Bjr

3) lim (e^cos x - e)/ x si x---> 0 forme 0/0

Règle de l' Hospital

=> lim (-sinx*e^cos x -1)/ 1=

je n'ai pas vu cette régle :s

[chuchi]

personne ??

[chuchi]

j'ai réussi la II/

personne pour la I et III ?

[chuchi]

tjs bloqué par l'équation et le II / ;s

[Huppasacee]

Bonjour

comme tu l'as fait pour les fonctions rationnelles ( des polynômes au numérateur et au dénominateur ) , il faut mettre en facteur , au numérateur , la fonction avec la plus forte croissance . Pareil au dénominateur
Tu pourras ensuite conclure

[chuchi]

c'est à dire e?? mais le cos me géne

[Huppasacee]

Donc , c'est pour la III ?

Pour l'équation , tu calcules le discriminant et tu appliques les formules , qu'as tu comme z1 et z2 ?

[Huppasacee]

Pour la III, donc :

quelle est la définition du nombre dérivé d'une fonction en un point d'abscisse a ?

soit la fonction g(x) =
Appliquons la définition du nombre dérivé au point d'abscisse 0

[chuchi]

Donc , c'est pour la III ?

Pour l'équation , tu calcules le discriminant et tu appliques les formules , qu'as tu comme z1 et z2 ?

j'aboutis a :

[chuchi]

Pour la III, donc :

quelle est la définition du nombre dérivé d'une fonction en un point d'abscisse a ?

soit la fonction g(x) =
Appliquons la définition du nombre dérivé au point d'abscisse 0

donc

et ca ca vaut g'(0) ??

[chuchi]

Pour la III, donc :

quelle est la définition du nombre dérivé d'une fonction en un point d'abscisse a ?

soit la fonction g(x) =
Appliquons la définition du nombre dérivé au point d'abscisse 0

donc

et ca ca vaut g'(0) ??

[chuchi]

personne?? ya qu'à vérifier :doh:

[CDuce]

Salut ;
Pour la première question ; On doit trouver d'abord les solutions :
Voila donc on a :
z^2 + e^{-\alpha} z + e^{-2\alpha} = 0

Delta= -3e^-2x ; j'ai remplacer ici le alpha par un x

La racine de Delta = i(rac3) e^-x= (i rac(3))/e^x Du cours ;)

Les solutions :

Z=-[(i rac(3) + e^(2x))]/ (2e^x) ; Z'=[(i rac(3) - e^(2x))]/ (2e^x)

Ce qui reste et simple si en écrit: irac(3) sous forme de : e^...on pourrai trouver facilement l'argument puis le module de ceux ci .

Donc voila la première partie :)

[CDuce]

II)
PS: s'il s'agit des complexes je crois que t'as oublié un: i quelque part !!?

La formule d'Euler :

|2cos(x)=e^ix + e^-ix
|2isin(x)=e^ix - e^-ix

Maintenant tu peux bien simplifier ta limite, ensuite avec un changement de variable tu trouvera : +~ ; lim X->+~ (tanX)/X = 1 .

Si ce n'était que de simple exponentiels tu fera bien de factoriser par e^x en au haut et en bas t'aura un 1 .

Alors Pour la III partie j'aimerai bien savoir si c'est un exponentiel ou non !!

[chuchi]

II)

La formule d'Euler :

|2cos(x)=e^x + e^-x
|2isin(x)=e^x - e^-x

Maintenant tu peux bien simplifier ta limite, ensuite avec un changement de variable tu trouvera : +~ ; lim X->+~ (tanX)/X = 1 .

j'ai jamais vu ces formules :mur:

[chuchi]

Salut ;
Pour la première question ; On doit trouver d'abord les solutions :
Voila donc on a :
z^2 + e^{-\alpha} z + e^{-2\alpha} = 0

Delta= -3e^-2x ; j'ai remplacer ici le alpha par un x

La racine de Delta = i(rac3) e^-x= (i rac(3))/e^x Du cours

Les solutions :

Z=-[(i rac(3) + e^(2x))]/ (2e^x) ; Z'=[(i rac(3) - e^(2x))]/ (2e^x)

Ce qui reste et simple si en écrit: irac(3) sous forme de : e^...on pourrai trouver facilement l'argument puis le module de ceux ci .

Donc voila la première partie

je comprend pas trop, la formule c'est :



mais

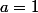
[CDuce]

En fait j'ai oublié un i ; c'est plutot e^ix / e^-ix .
Sinon la formule d'Euler c'est dans le cours enfin pour moi !!

[CDuce]

Alors pour la racine de Delta je crois que c'est : i rac(3) e^-x " c'est un -x " .