voila ma demo:je regarde l opérateur T defini par
=b_n)
.Je veux montrer que T est bijectif.Deja,T est une isométrie,donc est injectif et d image fermée.Ensuite T s écrit Id+S ou S est l opérateur défini par
=b_k-a_k)
.Comme par hypothese,
||^2)
est finie,S est donc un opérateur de Hilbert-Schmidt,donc compact.Soit maintenant x orthogonal a
)
.Les

sont 2 a 2 ortogonaux et de normes constante.Par compacité de S,la suite
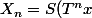=T^nx-T^{n+1}x)
doit avoir une sous suite convergente.Mais

est orthogonal a
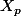
si p>n+1,donc la seule limite possible est 0,et T étant une isométrie,on doit avoir en fait
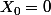
,ie Tx=x,donc x appartient aussi a Im(T) donc x=0.Im(T) est donc dense,donc egal a tout l espace.T est bien bijectif,(b_n) est donc une base
et
telles que la série de terme général
soit convergente.
est dense dans H. Que dire de
?
