Inégalité

[MathMoiCa]

Boh... une 'tite inégalité. Quelqu'un l'a résolue d'une assez jolie manière sur un autre forum. Voyons ce que vous proposez ^^

x+y=1, x et y > 0
Montrer que

P.S. : évitez la solution où il "suffit" de remplacer x=1-y, ce n'est pas élégant :id: Et disons que c'est de l'algèbre qu'on demande, pas des dérivées ^^


M.

[Nightmare]

Salut :happy3:

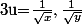Cauchy-Schwartz appliquée aux vecteurs et .

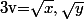Cauchy-Schwartz nous permiet d'écrire que

Or, , ,

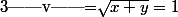
D'où :

soit :
.

Ou encore,

[MathMoiCa]

Pas mal Cauchy-Schwartz :id:

Valà la méthode que j'ai vue :


On déduit de ça que

Puis :



M.