Petit angle

[Imod]

Un petit problème simple si on le prend par le bon bout .

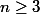
On se donne un entier et points du plan . Montrer que parmi ces points , on peut en choisir trois , et tels que .

Bon courage :zen:

Imod

[killer_mo]

Si on suppose l'inverse tel que pour tous A, O, B choisi, l'angle (AOB) > 180/n

alors l'angle (OBA) et l'angle (BAO) seront aussi > 180/n car on aurait pu les choisir eux étant donné que c'est pour tous 3 points

on sait que la somme des angles intérieurs d'un triangle est de 180 et
que la somme des angles intérieur du triangle AOB sera > (3*180)/n

or cela est impossible car n étant plus grand ou égale a 3
la somme des angles de AOB sera plus petite ou égal a 180
étant donné la contradiction à laquelle on aboutit en supposant l'inverse
on voit que l'énoncé principale est vrai.

J'espere j'ai pas fait d'erreur

[Imod]

Il me semble que tu as pris ton inégalité à l'envers :we:

Sauf erreur tu aboutis à qui n'est pas une contradiction pour .

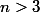
Imod

[nodgim]

Soit n points du plan. Le polynome convexe extérieur de ce nuage de points comprend k<=n points. Le plus petit angle intérieur de ce polynome est au plus égal à Pi(k-2)/k. On remarque que (k-2)/k<=(n-2)/n. Or, à partir de ce sommet on a (n-1) segments, les 2 segments du polynome et les (n-3) diagonales. Donc (n-2) angles. Le plus petit angle qui arrive sur ce sommet est donc au maximum de:
Pi(k-2)/k(n-2)<=Pi(n-2)/n(n-2)=Pi/n

[Imod]

C'est bien ça nodgim :++:

Très facile quand on s'y prend bien :id:

Imod