Exercice sur la fonction ln
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 20:39
par bombastus » 02 Avr 2009, 20:39
Oui et son signe?
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 20:55
par bombastus » 02 Avr 2009, 20:55
Tu essaies de deviner? elle n'est pas négative sur [3,+infini[
 par tagada-chantilly » 02 Avr 2009, 21:00
par tagada-chantilly » 02 Avr 2009, 21:00
non pas du tout c'est en faisant un tableau de variation que j'en ai déduit le signe de f''
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 21:13
par bombastus » 02 Avr 2009, 21:13
Si tu veux une correction, essaie de détailler tes réponses.
Comment as-tu trouver qu'elle est négative?
 par tagada-chantilly » 02 Avr 2009, 21:19
par tagada-chantilly » 02 Avr 2009, 21:19
en regardant le signe du numérateur négatif jusqu'à 7 puis positive et le signe du dénominateur positif donc f'' négative
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 21:24
par bombastus » 02 Avr 2009, 21:24
Ben, non, tu l'as écrits toi-même : le numérateur est négatif pour x<7, puis positive, donc f'' n'est pas toujours négatif!!!
 par tagada-chantilly » 02 Avr 2009, 21:34
par tagada-chantilly » 02 Avr 2009, 21:34
f'' serait donc positif sur x<7 et négatif x>7
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 21:36
par bombastus » 02 Avr 2009, 21:36
Non,
Pour 3(x-7)<0
et (x-3)^2>0
donc f'' est .....
Pour x>7 on a
(x-7)>0
et (x-3)^2>0
donc f'' est ....
 par tagada-chantilly » 02 Avr 2009, 21:39
par tagada-chantilly » 02 Avr 2009, 21:39
Pour 3(x-7)<0
et (x-3)^2>0
donc f'' est négatif
Pour x>7 on a
(x-7)>0
et (x-3)^2>0
donc f'' est positif
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 21:45
par bombastus » 02 Avr 2009, 21:45
Ok tu peux faire la suite
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 22:02
par bombastus » 02 Avr 2009, 22:02
Non, comment as-tu trouvé cela?
(Ca irait vraiment plus vite si tu détaillais un peu plus tes réponses au lieu que je te le demande à chaque fois...)
 par tagada-chantilly » 02 Avr 2009, 22:17
par tagada-chantilly » 02 Avr 2009, 22:17
j'ai cherché le signe de ln(x-3) qui est x0 pour x>4 ensuite j'ai pris le signe de
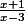
qui est positif on en déduit ainsi le signe de f'(x ) qui est faux il faut la aussi mettre sous le même dénominateur?
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 22:31
par bombastus » 02 Avr 2009, 22:31
tagada-chantilly a écrit:j'ai cherché le signe de ln(x-3) qui est x0 pour x>4 ensuite j'ai pris le signe de
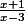
qui est positif on en déduit ainsi le signe de f'(x ) qui est faux il faut la aussi mettre sous le même dénominateur?
Effectivement ta méthode est encore fausse.
Mais ici même en mettant au même dénominateur, tu ne pourra pas en déduire le signe de f'.
Il faut que tu trouves le signe de f' à partir du tableau de variation de f'
 par tagada-chantilly » 02 Avr 2009, 22:32
par tagada-chantilly » 02 Avr 2009, 22:32
et comment fait-on pour trouver le signe d'un nombre à partir d'un tableau de variation je ne vois pas du tout
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 22:34
par bombastus » 02 Avr 2009, 22:34
As-tu fait le tableau de variation?
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 02 Avr 2009, 22:40
par bombastus » 02 Avr 2009, 22:40
Que vaut f'(7)? Ne peux-pas en déduire le signe de f'?
 par tagada-chantilly » 02 Avr 2009, 22:43
par tagada-chantilly » 02 Avr 2009, 22:43
ah ooui f'(7)>0 et comme c'est un minimum local la fonction est positive
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
qui est positif on en déduit ainsi le signe de f'(x ) qui est faux il faut la aussi mettre sous le même dénominateur?
