Suites...continuité et convergence.

[schyschy]

Bonsoir j'ai un qcm à faire en Maths. La première partie de propositions j'y sui parvenu mais je bloque sur la fin.

Voila l'énoncé;

On considère une suite positive et une suite définie par

Les propositions suivantes sont-elles vraies?

7-Pour tout n, .
8-Si la suite est convergente, alors la suiteet convergente.
9-Si la suite est croissante, alors la suite est croissante.
10-Si la suite est convergente, alors la suite est convergente.

[Mikou]

vrai-vrai-vrai-faux :)

[schyschy]

ok comment tu demontre les trois premières?
et tu peux me trouver un contre exemple pour la dermière qui est fausse?

Merci :we:

[abcd22]

Bonsoir !
Pour le 7, est positive, et .
Pour le 8, si tend vers , tend vers .
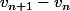
Pour le 9, calculer et montrer que c'est positif en utilisant le fait que est croissante.
Pour le 10, pour n'importe quelle suite qui tend vers l'infini, tend vers 1.

[schyschy]

merci beaucoup! :happy2:

[Mikou]

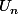
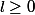
note que pour la 8) cela est vrai car si converge alors elle coverge vers or

[schyschy]

Merci pour le complément! :happy2:

[schyschy]

Quelqu'un pourrait-il m'aider pour la proposition 9 s'il vous plait? :marteau:

[abcd22]

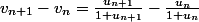
Pour le 9, on peut calculer , on réduit au même dénominateur :
tu devrais réussir à montrer que c'est positif là ?

[schyschy]

Ok merci beaucoup!
Juste une question pour la dix aidez moi à trouver un contre exemple.
On prend (Vn) convergente et il s'agit de montrer que (un) n'est pas forcément convergente.

[schyschy]

??? :marteau:

[abcd22]

On prend (Vn) convergente et il s'agit de montrer que (un) n'est pas forcément convergente.

On trouve non convergente telle que converge, et avec n'importe quelle suite qui tend vers l'infini, tend vers 1, donc ça donne un contre-exemple.