Principe du maximum

[cyclique]

Bonjour,
J'ai un exercice concernant le principe du max pour une fct sous harmonique (pour rappel f est sous harmo si son laplacien et 0 )
ce principe dit qu'une fct harmonique atteint son max sur le bord du domaine.

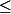
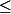
Sachant ceci, supposons que u est sous harmonique dans D (domaine) et supposons que v est harmonique dand D. Si uv sur le bord de D, alors on demande de prouver que uv dans D.

Je ne sais pas trop comment y arriver, comme v est harmonique on sait que son max et son min sont atteint sur le bord. De plus on sait que le max de v est également plus grand que celui de u (qui est également atteint sur le bord) mais pour ce qui est du reste je ne vois pas... :hein:

[Nightmare]

Salut :happy3:

Applique le principe du maximum à u-v ça semble bien marcher !

[ShakkaChan]

c'est pas u>v sur le bord et u>v qu'on doit montrer plutot que v>u ?
ca me parait bizarre car
voici mon raisonnement


tu a donc le principe du maximum qui dit que u et v son harmonique implique que le
maximum est atteint sur le bord
puisque u sous harmonique et v harmonique alors u-v est sous harmonique
or u-v>0 sur le bord donc par le principe du maximum u-v>0