Mesure versus capacité

[kazeriahm]

Bonjour bonjour,

en lisant ce poly http://www.iecn.u-nancy.fr/~munnier/enseignement/cours_edp.pdf sur les EDP, je tombe page 41 exercice 2.18 sur la notion de capacité.

Je cite :

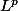
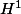
Dans les espaces , deux fonctions qui diffèrent seulement sur un ensemble de mesure nulle sont égales. Ce n'est plus le cas dans les espaces de Sobolev. Dans les espaces , la bonne notion est celle de capacité . Par exemple, l'ensemble n'est pas de capacité nulle dans mais le point est de capacité nulle dans . Ceci entraine que mais que où est un ouvert de contenant (0; 0).

Quelqu'un connait cette notion de capacité ? Google est improductif et je trouve pas ca dans les rares bouquins qui parcellent mon armoire

[kazeriahm]

je me rappelle plus comment on fait le symbole \ en Latex sorry

[Nightmare]

Salut :happy3:

Notre ami Quinto pourrait t'en parler mieux que moi s'il était là. De ce que j'ai pu comprendre :

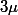
On se donner une mesure a support compact.

On définit son énergie par :
où d est une distance hyperbolique.

La capacité C(E) d'un ensemble mesurable E se définie alors par :


Il y a un rapport étroit entre la capacité et la mesure de Hausdorff.

[Clembou]

je me rappelle plus comment on fait le symbole \ en Latex sorry

\backslash : :happy2:

[kazeriahm]

Bon au cas où ca interesse du monde,

la notion de capacité sert à repérer des ensembles de mesure nulle, comme les fissures dans le plan ou de manière plus générale les courbes (les variétés de dimension n-1 ??), qui ne sont pas repérées par les L^p mais qui le sont par les H^s

bref...