Fonctions - Parité et ensemble de définition

[aurele59681]

Bonjour,

voici un exercice :

Dans chacun des cas déterminer l'ensemble de définition D de f et dire si la fonction f est paire, impaire ou ni paire ni impaire.


a) f(x) = x(x² - 1) +1

b) f(x) = cos (2x)

c) f(x) = x +

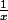
d) f(x) = sin (x²) ( un question : est-ce que sin² x et sin (x²) c'est la même chose ?)

(Pour la D , j'ai utilisé sin² x en admettant que se soit la même chose que sin (x²) )

Mes réponses :

a) Df =

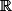
f(x) = x(x² -1) + 1

f(-x)= -x (-x² -1) +1
= -x (x² -1) +1
= - f(x)

Donc f(x) est impaire.

b) Df = [-;) ;;) ]

f(x) = cos (2x)

f(-x) = cos -2x
=cos 2x
= f(x)

Donc f(x) est paire.

c) Df = R*

f(x) = x +

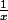
f(-x) = -x +
= -f(x)

donc Impaire.

d) Df = [-;) ;;) ]

f(x) = sin (x²)

f(-x) = sin (-x²)
= - f(x)

donc Impaire.

Conclusion

J'aimerais savoir si cela est exact ?

merci d'avance

[Sa Majesté]

Salut

C'est bon sauf la d
sin²(x) = (sin(x))², ce n'est pas pareil que sin(x²)

Et pour la b et la d, Df=R

[aurele59681]

en fait pour la D dans l'exercice s'est écrit comme ceci :

d) f(x) = sin (x²)

donc mon d) est exact je pense , nn ?

merci

[Sa Majesté]

Non car (-x)²=x²