DM de mathématiques de spécialité de 1ère !

[oblivius]

Bonjour à tous, je viens de découvrir ce forum et j'ai du mal a l'avouer mais il est mon dernier espoir pour réussir mon DM.
Alors voila cela fait 2 semaines que j'ai reçu ce DM à faire, et cela fait également 2 semaine que je prend tout mon temps libre pour me plonger dans sa résolution. Et je n'est réussi qu'a résoudre le premier exercice et une partie du second. Ce devoir est a rendre pour le mardi 31 mars, j'ai donc vraiment attendu le dernier moment pour sollicité votre aide.

Je vais vous détaillé ci-dessous le devoir :

EXERCICE 1 : QCM

1/ Dans un repère orthonormé de l'espace, y=3x-5 est une équation cartésienne de: A) droite B) plan C) surface non plane
2/ Dans un repère orthonormé de l'espace, 2y-2x=3 est l'équation d'un plan parallèle à: A) (Oz) B) (Ox) C) (Oy)
3/ Dans un repère orthonormé de l'espace, y=3 est l'équation d'un plan parallèle à: A) (xOz) B) (yOz) C) (xOy)

EXERCICE 2 : l'espace est rapporté au repère orthonormal (O;i;j;k).

Les points I(1;0;4),J(2;0;2) et K(0;3;0). Soit n(2;2;1)

1/ Montrer que n est un vecteur orthogonal aux vecteurs IJ et IK
2/ En déduire que n est un vecteur normal au plan (IJK)
3/ Montrer qu'une équation du plan (IJK) est 2x+2y+z=6
4/ les points A(-1;1;6) et B(1;1;1) appartiennent-ils au plan (IJK) ?

EXERCICE 3 :

1/ Dans le repère (O;i;j;k) ci-contre, placer les points A,B et C, points respectifs d'intersection du plan (P) d'équation : 3x+2y+z-6=0 avec les axes et représenter le plan (P)
2/ Calculer la cote du point N d'abscisse 3 et d'ordonnée 1 sachant que ce point appartient au plan (P)
3/ Déterminer les coordonnées de deux points Q et R de cote 4 de (P).

EXERCICE 4 : Dans un repère orthonormal (O;i;j;k) les cinq points A(5;0;6), B(-5;0;6), C(-5;8;0), D(5;8;0) et E(0;10;11).

On se propose de montrer que EABCD est une pyramide régulière de sommet E ( toutes les arêtes issues de E ont la même longueur à base carrée.

1/ Calculer les coordonnées des vecteurs AB DC et AD
2/ Prouver que ABCD est un parallélogramme.
3/ Prouver que les vecteurs AB et AD sont orthogonaux et que AB=AD. Justifier que ABCD est un carrée.
4/ Calculer les coordonnées des vecteurs AE, BE, CE et DE.
5/ Prouver que AE=BE=CE=DE. En déduire que EABCD est une pyramide régulière à base carrée.


Voila, je fait maintenant appel à votre générosité, j'attends bien sur de l'aide mais vu le temps qu'il me reste pour le rendre, une résolution du DM ou de quelque exercice me réjouirai au plus haut point. Voici mon adresse MSN pour que vous puissiez m'envoyer vos aides : supprimé.

Un grand merci pour votre attention, et votre compréhension. øB£iiV!ù$

[Timothé Lefebvre]

Voila, je fait maintenant appel à votre générosité, j'attends bien sur de l'aide mais vu le temps qu'il me reste pour le rendre, une résolution du DM ou de quelque exercice me réjouirai au plus haut point. Voici mon adresse MSN pour que vous puissiez m'envoyer vos aides : supprimé.

Bonsoir,

on croit rêver !!
Il n'en est pas question !

As-tu lu le règlement au moins ?
As-tu commencé à chercher ?

:triste:

[busard_des_roseaux]

salut,

tout cela est bien étrange. c pas sorcier.

Pour obtenir l'intersection du plan (P) d'équation 3x+2y+z-6= 0
avec l'axe x'Ox , cet axe a pour équation
(y=0 et z=0) . Il suffit de calculer la cote z du point.

même chose pour les autres axes.

(3)
On dispose d'un produit scalaire dans l'espace
u.v = xx'+yy'+zz'
où (x,y,z) sont les coordonnées de
où (x',y',z') sont les coordonnées de

grâce à ce produit scalaire, on peut calculer des distances



en sachant calculer des distances, on peut démontrer
que des parallèlogrammes sont des rectangles ou des losanges.

Pour montrer que ABCD est un parallèlogramme, il suffit de vérifier que
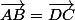, en utilisant les coordonnées.