Salut, j'ai un petit soucis sur un exo portant sur les polynômes que voici :
Résoudre P(X)-P(X-1) = X² dans R[X]
Je tatonne un peu sans succés...
J'ai éssayé d'éxprimer P(X) et P(X-1) pour que la différence donne X², mais je ne dois pas avoir la bonne démarche puisque je n'arrive à rien...
Merci d'avance pour l'aide !
Polynômes
9 messages
- Page 1 sur 1
Déjà le degré de P devrait être clair (c'est 3  ) en regardant juste le monôme de plus haut degré. Ensuite tu remplaces et tu identifies (méthode buf qui marche).
) en regardant juste le monôme de plus haut degré. Ensuite tu remplaces et tu identifies (méthode buf qui marche).
Ou si P est sol alors P + cst est sol donc on peut prendre P(0)=0 et P(n) =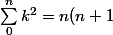(2n+1)/6) pour tout n et P coïncide avec X(X+1)(2X+1)/6 sur un ensemble infini (on est dans R).
pour tout n et P coïncide avec X(X+1)(2X+1)/6 sur un ensemble infini (on est dans R).
Le refaire dans Z/nZ[X]
Ou si P est sol alors P + cst est sol donc on peut prendre P(0)=0 et P(n) =
Le refaire dans Z/nZ[X]
ThSQ a écrit:Déjà le degré de P devrait être clair (c'est 3) en regardant juste le monôme de plus haut degré. Ensuite tu remplaces et tu identifies (méthode buf qui marche).
Une dernière chose, le fait que P soit de degré 3 me parait logique, sauf qu'on me demande de justifier...Il y a une vrai justification?parce que l'expliquer "avec les mains " ça va, mais sur papier je bloque un peu.
Merci
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
