Suites numeriques, algebriques, geometriques

[qetuo]

bonjour tout le monde, je suis en premiere s et j'ai un ds mardi sauf que je n'ai pas tres bien compris le cours!
Vous pourriez m'expliquez un peu ce que sont une suite numeriques, algebriques ett geometriques.

merci d'avance

[busard_des_roseaux]

salut,

Vous pourriez m'expliquez un peu ce que sont une suite numeriques, arithmétique et géometriques.

oui, un tout petit peu,alors :zen:


exemple 1:

regarde ces valeurs:

2;5;8;11;14;17;20;23;26;29;32;35.......

ce sont des termes d'une suite arithmétique. On passe d'un terme au suivant en ajoutant 3.
3 est la raison de la suite. On note r=3.

On peut numéroter ces valeurs. Un numéro s'appelle un indice. En général, on numérote à partir de l'indice zéro. ce qui donne:



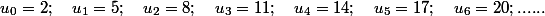
comme on passe d'un terme au suivant en ajoutant 3,on écrit
l'égalité
pour tout indice

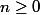
exemple 2:
regarde maintenant ces autres valeurs:
1; 2; 4; 8; 16; 32; 64; 128; 256; 512; 1024; 2048; 4096; 8192;.....

On passe d'un terme au suivant en multipliant par 2.
Ce sont les termes d'une suite géométrique. La raison est 2. On note q=2.
On numérote aussi les termes de cette nouvelle suite à partir de l'indice zéro.



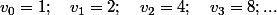
içi, on écrira:
pour tout indice (*)

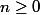Une égalité comme (*) s'appelle
une "relation de récurrence". Si représente un indice,
est alors l'indice suivant .

une relation de récurrence permet de calculer les termes de la suite
de proche en proche. Connaissant la valeur de , on peut calculer la valeur de 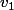, puis celle de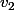
en remplaçant l'indice par zéro,puis par 1,.. dans la relation de récurrence.

Comme nous avons étudié deux suites, la première était notée par , la seconde était notée . On dit que l'on définit
la suite (v) de terme général .
Içi, vaut .

exemple 3:
Le 1er terme est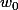 . Il vaut 27.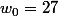

On définit la suite par la relation de récurrence
si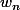 est pair,
sinon,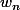 est impair, alors

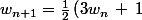essaye de calculer la valeur des termes suivants .

Cette suite n'est ni arithmétique ni géométrique. Elle s'appelle "suite de Collatz" ou "suite de Syracuse", du nom de l'université américaine.

Elle a été inventée par un ami du mathématicien Collatz, qui l'a ensuite
proposée, pour étude, aux matheux de l'université de Syracuse.
Cette suite tire son origine de la théorie des graphes. :zen:

remarque
attention , ne pas confondre et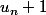
Par exemple, pour la suite de l'exemple 1,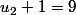 et

[qetuo]

merci beaucoup...desole pour le retard, j'ai eu quelques problemes de connexion