Demontation trés difficile
Réponses à toutes vos questions du CP à la 3ème
-
hip_adib
- Membre Naturel
- Messages: 34
- Enregistré le: 24 Nov 2008, 21:52
-
 par hip_adib » 28 Mar 2009, 12:13
par hip_adib » 28 Mar 2009, 12:13
bonjours tous le monde:
je presente ce difficiel exercicedont j'ai passé 2h bloqué devant la feuille sans bougé le stylo.
l'exercice:l'enoncén: un nombre naturel (appartient à N) de sorte que n est plus grand ou égale à 2 (n

2).
A1 et A2 et.....An sont des nombres reél (appartient à R) de sorte que A1*A2....An=1.
la questiondemontre que (1+A1)(1+A2)....(1+An);) 2^n
et mille merci pour votre patiente.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Mar 2009, 12:50
par Zweig » 28 Mar 2009, 12:50
Salut,
Ton résultat n'est vrai que si tes réels

sont positifs (car si on prend
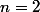
et
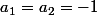
, alors l'inégalité est fausse).
On a

pour tout naturel

car
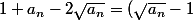^2 \geq 0)
Ainsi en faisant le produit on obtient :
\cdots(1+a_n)\geq2^n\sqrt{a_1a_2\cdots a_n} = 2^n)
L'égalité est atteinte lorsque
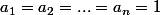
-
hip_adib
- Membre Naturel
- Messages: 34
- Enregistré le: 24 Nov 2008, 21:52
-
 par hip_adib » 28 Mar 2009, 13:14
par hip_adib » 28 Mar 2009, 13:14
Zweig a écrit:Salut,
Ton résultat n'est vrai que si tes réels a_n sont positifs.
On a

pour tout naturel

car
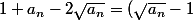^2 \geq 0)
Ainsi en faisant le produit on obtient :
\cdots(1+a_n)\geq2^n\sqrt{a_1a_2\cdots a_n} = 2^n)
j'ai pu conclure que (1+a1)(1+a2)...(1+an);) 2 mais comment on peut conclure que (1+a1)(1+a2)...(1+an);) 2^n
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Mar 2009, 13:18
par Zweig » 28 Mar 2009, 13:18


...

Tu fais le produit de toutes ces inégalités (y'en a

), tu obtiens donc :
\cdots(1+a_n)\geq2\cdot2\cdots2\sqrt{a_1a_2\cdots a_n})
ou encore
\cdots(1+a_n)\geq 2^n\sqrt{1} = 2^n)
-
hip_adib
- Membre Naturel
- Messages: 34
- Enregistré le: 24 Nov 2008, 21:52
-
 par hip_adib » 28 Mar 2009, 13:26
par hip_adib » 28 Mar 2009, 13:26
merci j'ai compris
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Mar 2009, 13:27
par Zweig » 28 Mar 2009, 13:27
Au plaisir :zen:.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
