[T.S ]Probabilité discrètes

par **opxsl** » 26 Mar 2009, 19:28

Bonsoir à tous, alors voila un dm que j'ai à rendre malheuresement pour demain, et j'bloque totalement à partir du 2).

Je poste le mon dm à travers un lien où je l'ai hébergé et mes réponses ci dessous:

a) -> Loi binomiale
b) paramètres : n = 24 ; p = 5/12
c) p ( X=12) = 0.115 ( environ )
d) Épreuve de Bernoulli donc : P ( x = 1 ) p = 5/12
e) p ( X =2) = 2* p = 0.83 ( je n'suis pas sur )
Non, elle n'est pas assez faible pour être négligeable.

A partir de là, j'bloque jusqu'à la fin.

Merci d'avance de votre aide.

http://img145.imageshack.us/my.php?image=dsc00858.jpg

par **mathgaussmath** » 26 Mar 2009, 21:07

Bosoir Opxls,
Le but de ton exo est de demontrer que:
"Lorsque n tend vers l'infini et que p tend vers 0 avec np = a, la loi binomiale converge vers une loi de Poisson de paramètre a "....
Alors, commençant par la question 1-c), j'ai pas de reponse mais je sais que ta reponse n'est pas juste, car X represente le nbr de feuilles dans tte la journée et non pas dans une heure.
Question 2:
a)X suit tjr une binomiale(86400,

); la difference ici c'est que on compte chaque seconde au lieu de chaque heure. Avec la meme esperance,

(X)=10, on aura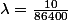

(fais ce calcul..)
b)

(X=12)= ...(formule de binomiale)
c)je sais tjr pas comment faire :marteau:
Question 3: Voilà mantenant c'est la généralisation
a) la loi de X est binomiale de paramètres: N et

. D'où le resultat demandé.
b)

, il faut montrer que

, mais je sais pa comment
c) cette limite n'est que la derivée de ln au point 1 qu'est égale à: 1.
d)On a:

, alors si on choisit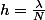

on aura bien:

e)la loi des proba de nbre de feuilles est la loi de Poisson de parametre

:

Voilà...j'epère que cela pourrait t'aider...

par **opxsl** » 26 Mar 2009, 21:58

Merci de ta réponse.

Mais j'vois toujours pas ce que j'dois faire dans le 3) a ) ?

par **mathgaussmath** » 26 Mar 2009, 22:04

opxsl a écrit:Merci de ta réponse.

Mais j'vois toujours pas ce que j'dois faire dans le 3) a ) ?

3-a)
la loi de X est binomiale de paramètres: N et

. D'où le resultat demandé:

par **opxsl** » 26 Mar 2009, 22:05

J'écris simplement ça sur ma copie? Où j'dois faire un calcul ? :marteau:

Ok, donc pour la 2)a) j'trouve p = 1.16*10^-4 et n = 86400

b) --> 0.095 en appliquant la loi binomiale
c) j'ai pensé à la probabilité que deux feuilles tombent à la même seconde soit : (1/8640)²

Mais l'énoncé nous demande la probabilité que deux feuilles ne tombent pas à la même seconde.

par **mathgaussmath** » 26 Mar 2009, 22:16

opxsl a écrit:c) j'ai pensé à la probabilité que deux feuilles tombent à la même seconde soit : (1/86400)².

??

opxsl a écrit:Mais l'énoncé nous demande la probabilité que deux feuilles ne tombent pas à la même seconde.

je pense pas, la question est bien la meme que dans 1-a), sauf que c'est formuler d'une autre façon, parce que l'hypothèse est tjr qu'on a une seule feuille par seconde, donc il faut verifier que notre hypo est valide...enfin c'est ce que je pense

par **opxsl** » 26 Mar 2009, 22:25

Ok.Pour la question 3) a j'écris simplement ça? :

la loi de X est binomiale de paramètres: N et

. D'où :

par **opxsl** » 26 Mar 2009, 22:36

Je n'comprends pas comment tu fais pour la 3) c ) pour obtenir 1. Vu que divisé par zéro n'est pas possible.

par **mathgaussmath** » 26 Mar 2009, 22:36

Alors, pour 3-a):
On decoupe la journée en N intervalles, dans chaque intervalle on suppose que soit une seule feuille qui tombe soit rien, on suppose encore que les chutes sont independantes. Soit X la variable aléatoire qui compte le nbr de feuille pendant la journée. On voie bien que X suit une binomiale de parametres N et p. Mantenant, déterminons p:
On sait que le nombre de feuilles moyen est

, qui n'est que l'eperance mathematique de notre variable X, et on sait que:

=Np, ce qui donne:

=Np donc p=

.
Donc, la proba demandée est:....

par **opxsl** » 26 Mar 2009, 22:45

Comment appliquer la loi binomiale alors qu'on a pas la valeur de lambda et de N ?

par **mathgaussmath** » 26 Mar 2009, 22:48

justement, pour 3-c) on ne calcul pas la limite directement car c une forme indeterminée!!!!!
mais, on sait que

Ici, f(x)=ln(x)....

par **mathgaussmath** » 26 Mar 2009, 22:54

opxsl a écrit:Comment appliquer la loi binomiale alors qu'on a pas la valeur de lambda et de N ?

Où-est ce que tu veux l'appliquer??
Ici, c'est une généralisation, pour dire que quand N tends vers l'infini alors la loi binomiale de parametres N et p converge vers une loi de poisson de parametre lambda = Np....

par **opxsl** » 26 Mar 2009, 23:01

Je dois donc écrire simplement :

la loi de X est binomiale de paramètres: N et

. D'où :

Je rajoute rien d'autres? Désolé je fatigue, :doh:

Pour c) On fait donc Ln(1)'=0 ?

par **opxsl** » 26 Mar 2009, 23:45

Encore un peu d'aide, s'il vous plait.

par **mathgaussmath** » 26 Mar 2009, 23:47

pour 3-a) essaie de reecrire tout ce que je t'ai ecrit, comme ça tu montre le raisonement; pour 3-c) je prefere aussi rappeler l'identité utilisée: on sait que lim... ici f(x)=ln(x) et donc la formule=ln'(1)=1...
bon courage!

par **opxsl** » 26 Mar 2009, 23:49

Ok, je t'ai envoyé un MP.

par **mathgaussmath** » 26 Mar 2009, 23:52

opxsl a écrit:Pour c) On fait donc Ln(1)'=0 ?

ecoute ln'(1)=1 et pas 0, car ln'(x)=

, donc pour x=1, ln'(1)=1....

par **opxsl** » 26 Mar 2009, 23:58

Exact, autant pour moi, j'avais calculé la dérivée de la constante Ln(1) soit la dérivée de 0 ^^...

Tu as lu mon message personnel?

[T.S ]Probabilité discrètes

[T.S ]Probabilité discrètes

Qui est en ligne