Exercice dérivées 1ere ES

[zeclem]

Bonjour, voila on me donne :

f fonction définie sur ]-3; infini [
f(x) = (x²+4x+2)/(x+3)

1; a) vérifier que pour tout x supérieur à -3,
f '(x) = (x²+6x+10)/(x+3)²

b) Etudier le signe de f '(x) selon x et établir le tableau de variation de f.

2. a) Déterminer les coordonnées du point d'intersection A de la courbe C avec l'axe des ordonnés.

b) Déterminer une équation à la tangente T à la courbe C au point A.

3.a) Déterminer les coordonnées du point d'intersection B de C avec l'axe des abcisses.

b) Déterminer une équation de la tangente T' à la courbe C au point B.

4. Tracer la courbe et les 2 tangentes avec 1 cm d'unité graphique.

Merci par avance de votre aide car je suis bloqué dès la 1ere question

Merci

[log86]

Bonjour, si et sont des fonctions, quelle est la dérivée de ?

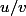
[zeclem]

je crois que c'est u'v-uv'/v²

mais je n'arrive pas à l'appliquer.
En fait se sont surtout ls questions d'après que je n'arrive pas a faire.
Merci d'avance de vos réponces

[mperthuisot]

soit u(x)=x^2+4x+2 alors u'(x)=?
et v(x)=x+3 alors v'(x)=?

[zeclem]

u '(x)= 2x+4
v '(x)= 1

[Piickles]

pour B) Il faut chercher le trinôme de la fonction f'(x) .. tu mets les racines que tu trouves dans un tableau de variation

rappel: si ton trinome est positif ..si tu as plusieurs racines F'(x) et du signe de "a" à l'extérieur des racines

[zeclem]

merci mai le pb c'est que je trouve le discriminant négatif

[Piickles]

Donc ta fonction n'a pas de racine.. alors elle est constante sur - l'infinie et + l'infinie