Etude de fonction numérique

par **sebirt** » 24 Mar 2009, 19:15

Bonjour, j' ai besoin d' aide pour un ptit exo de mah: voici le sujet

g(x)=-x+

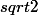
ln(x

)

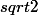
1) étudier g en 0 et en +infini

pour lim g quand x tend vers 0 j' ai trouvé -infini
mais pour g en +infini j' arrive pas à changer ka fonction pour ne plus tomber sur des formes indéterminées....

2) étudier les variations de g
la je ne suis pas sur que sa dérivées soit: g'=-1+1/(2

)+

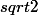
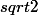
/x

par **axiome** » 24 Mar 2009, 19:19

Bonsoir,
Si tu factorisais par x pour la limite en + l'infini, tu t'en sortirais pas ?

par **sebirt** » 25 Mar 2009, 08:10

oui merci j' ai trouvé - infini donc g tend vers -infini quand x tend vers 0 et g tend vers - infini quand x tend vers +infini.
Mais pour lé dérivée je crois pas que ça soit juste car je ne tombe pas sur les bonnes variations, ça concordent pas avec les limites

par **axiome** » 25 Mar 2009, 10:52

Pour dériver ta fonction g, il faut que tu appliques la formule suivante :

par **sebirt** » 25 Mar 2009, 19:21

Oui, en effet j' avais fait une erreur de formule, j' ai trouvé la bonne dérivée:g'=
-1+V2/x

exercie résolu :)

Etude de fonction numérique

Etude de fonction numérique

Qui est en ligne