Leger probleme d'integrale

[alf]

Bonjour, je suis étudiant en deuxieme années de B.T.S., et les maths et moi ca fait trois....
Bref je ne vais pas m'étaler sur ma triste histoire avec les maths sinon vous allez sortir vos mouchoirs....


Je cherche simplement a integrer x/(x^4 + 1) , en remplacant x par u^2.


Je ne sait pas si il faut que je me lance dans:

1/(u^2 * u +1) ou x/(x^2 + 1)


Un petit coup de main merci.

[abcd22]

Bonjour, ça me semble plus logique de poser u=x², donc du = 2xdx, et

[alf]

J'ai bien compris merci, mais alors dans ce cas la, quel est la facon d'integrer?

[abcd22]

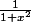
On a une primitive usuelle pour , c'est Arctan !

[alf]

ah oui je sors le 1/2 d'accord bien merci.

[alf]

pourquoi les limites de l integration sont au carré?

[abcd22]

C'est la formule de changement de variable, si x varie entre a et b et qu'on pose u=x², u variera entre a² et b² (il faut aussi que a et b aient le même signe pour que ça soit bon, pour que x² soit une bijection de [a,b] dans [a²,b²] (ou [b²,a²])).