bonjour,
khaledFB a écrit:BONJOUR !! je cherche un peu d'aide pour cette exercice :
n


,
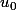

[0,B[ et

=g(Un)+(1/2).
1) Montrer que

n


,on a Un

[0,B[
2) Étudier la monotonie de la suite (Un). conclure.
3) montrer

n


,on a : |Un-B|

^n)
|

-B|
4) calculer alors

on a g'(x)

(1/2) et on a 1



2
bon j'ai trouvé la réponse sur la première et la deuxiéme question ( la suite est croissante et elle est convergente[monotone et minoré par B])
mais je suis bloqué dans la 3éme et la 4éme :hum:
voilà ce que j'ai trouvé:
Vérifions ,

n n


,
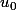

[0,B[(vrai)
suppesons : |Un-B|

^n)
|

-B|
démontrons : |
)
-B|

^(n+1))
|

-B|
on a |Un-B|

^n)
|

-B|
(1/2)|Un-B|

^(n+1))
|

-B|
on a
g(Un)+(1/2)=)
et g'(x)

(1/2)
donc *|
)
-(1/2)-B|

(1/2)|Un-B|* comment ça ??????
voilà il me reste le (-1/2) qui me gène ,si quelqu'un peu me montrer comment le faire ou me montrer ma faute ,ça sera cool :ptdr:
merci BCP
bon, tout d'abord tu as dit
g(Un)+(1/2)=)
pourquoi il y a ce -1/2 ??
- pour cette même question 3. il faut partir en posant f(x)=g(x)+1/2
tu applique le TIAF, et tu remplace x par Un. ça marche tout seul.
-pour le calcule de la limite, on par de l'inegalité de 3, on remplace n= 1;2;3; ... n-1. et tu multiplie membre à membre. en suite tu remplace U0 par ça valeur (que j'en suis sur tu l'as par calcul ou dans l'ennoncé).
le résultat doit etre normalement 0 (zéro).
je te laisse le plaisir de faire les calcules.
