Bonjour,
Je dois calculer l'intégrale de 0 à Pi de ln(1-2acosx+a²)dx avec a>1.
Mon idée était d'utiliser la formule des sommes de Riemann, en l'occurrence j'ai posé la fonction f(x)=ln(1-2acosx+a²) puis je sais que si f est continue sur [0,Pi] mon intégrale est égale à la limite quand n tend vers +infini de: Pi/n*Somme(i=1 à n) de ln(1-2acos(i*(Pi/n))+a²)
Pour la continuité de f j'ai montré que (1-2acosx+a²)>0 sur [0,Pi] donc le ln est définit et donc f est continue sur [0,Pi]
Mon problème se situe au niveau du calcul de la somme où j'avoue avoir de très gros problème dans ce genre de calcul.
J'espère que vous pourrez m'aider merci. :happy2:
Intégration sur un segment.
4 messages
- Page 1 sur 1
Bonjour,
ingrédients
1)
forme canonique du trinôme
+a^2=(a-cos(x))^2+sin^2(x))
2)
on doit calculer le produit des)^2+sin^2(\frac{k\pi}{n}))
que l'on interprète comme le carré du module du nombre complexe

on doit donc calculer le produit des
(a-e^{- i \frac{k\pi}{n}}))
3) le produit , juste avec les exponentielles et sans les "a" est connu
car ces exponentielles sont les racines 2n-ièmes de l'unité,
racines du polynome=x^{2n}-1)
(dessiner un cercle trigo, placer les 2n racines de l'unité)
les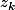 et
et  sont donc racines (par translation) du polynôme
sont donc racines (par translation) du polynôme
=P(a-x))
on connait donc leur produit en calculant ....
tu devrais trouver un résultat qui, (g pa fé les kalkuls),
ressemble peu ou prou à)
ingrédients
1)
forme canonique du trinôme
2)
on doit calculer le produit des
que l'on interprète comme le carré du module du nombre complexe
on doit donc calculer le produit des
3) le produit , juste avec les exponentielles et sans les "a" est connu
car ces exponentielles sont les racines 2n-ièmes de l'unité,
racines du polynome
(dessiner un cercle trigo, placer les 2n racines de l'unité)
les
on connait donc leur produit en calculant ....
tu devrais trouver un résultat qui, (g pa fé les kalkuls),
ressemble peu ou prou à
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
