Opérateur adjoint !

par **barbu23** » 07 Mar 2009, 19:13

Bonjour à tous : :happy3:
Soit :

un espace de Hilbert :
Soit :

un operateur linéaire sur

Je voudrai savoir pourquoi si le rang de

est fini implique que : le rang de

est fini , sachant que :

Merci d'avance de vos reponses ! :happy3:

par **franky4doigts** » 07 Mar 2009, 19:20

Bonjour. Tu devrais pouvoir montrer que A et A* ont même rang

par **barbu23** » 07 Mar 2009, 19:56

On a :

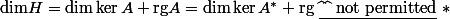
Cette formule peut servir à quelques choses dans la preuve de cette proposition ?
Je ne vois pas comment faire pour la suite : c'est pas évident du tout ! :hum: :lol2:

par **ThSQ** » 07 Mar 2009, 20:11

barbu23 a écrit: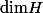

On est en dimension finie ??? (quel est le pb de montrer que u* est de rang fini alors ?

)

par **kazeriahm** » 07 Mar 2009, 22:20

Le théorème du rang n'est vrai qu'en dimension finie, sinon il n'a pas de sens...

par **barbu23** » 07 Mar 2009, 22:43

Ah oui c'est vrai !

par **yos** » 07 Mar 2009, 22:53

Tu as ImA* isomorphe à H/KerA*.

par **barbu23** » 07 Mar 2009, 23:16

Non ?
A - t - on vraiment :

?

par **yos** » 07 Mar 2009, 23:28

barbu23 a écrit:A - t - on vraiment :
?

Drôle d'idée. Non.

Mais par contre

par **barbu23** » 07 Mar 2009, 23:35

:lol2:
Merci yos :

par **barbu23** » 07 Mar 2009, 23:37

On a plutot :

non ?
car :

par **yos** » 08 Mar 2009, 00:22

barbu23 a écrit:On a plutot :

non ?

Ben c'est ce que j'ai écrit. L'orthogonal est évidemment pas sur le A, donc les parenthèses sont implicites. Cela dit tu as raison de les mettre.

barbu23 a écrit:car :

Là c'est des isomorphismes et pas des égalités. Par contre le premier membre égale le troisième.

Opérateur adjoint !

Opérateur adjoint !

Qui est en ligne