Système orthonormé !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 18:50
par barbu23 » 28 Fév 2009, 18:50
Bonjour :
Je voudrai savoir pourquoi, dans :
 = \{ f \hspace{2cm} | \hspace{2cm} \int_{0}^{1} f^{2} dt = \int_{0}^{1} f(t) g(t) dt $)
la famille :
)_{n \in \mathbb{Z}} $)
est orthonormée avec :

:
 = e^{2\pi i nt} $)
Merci infiniment !
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 28 Fév 2009, 18:55
par kazeriahm » 28 Fév 2009, 18:55
Il suffit de faire le calcul du produit scalaire et de distinguer les cas selon que m=n ou non.
Tu peux même montrer que c'est un système total de L^2.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 18:56
par barbu23 » 28 Fév 2009, 18:56
Pour

:
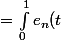 e_{m}(t) dt = \int_{0}^{1} e^{2 \pi i nt} e^{2 \pi i mt} dt = \int_{0}^{1} e^{2 \pi i (n+m) t} dt = \frac{1}{2 \pi i (n+m)} [e^{2 \pi i (n+m) t}]_{0}^{1} = \frac{1}{2 \pi i (n+m)} (e^{2 \pi i (n+m)}-1) = \frac{1}{2 \pi i (n+m)} (1-1) = 0 $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 18:58
par barbu23 » 28 Fév 2009, 18:58
Par contre quant

:
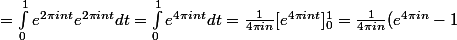 = 0 $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 19:02
par barbu23 » 28 Fév 2009, 19:02
kazeriahm , tu peux me dire si c'est juste ou non ?
Parceque : même quant

le produit scalaire est egale à :

! n'y'a-t-il pas une erreur quelques part ?
Merci d'avance ! :we:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 19:10
par barbu23 » 28 Fév 2009, 19:10
up ! :we:
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
 par R.C. » 28 Fév 2009, 19:11
par R.C. » 28 Fév 2009, 19:11
Il faut conjuguer g quand tu prend l'intégrale pour ton produit scalaire... et refaire les calculs!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 19:18
par barbu23 » 28 Fév 2009, 19:18
Ah oui, c'est vrai ! merci beaucoup "R.C." ! :happy2:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 19:45
par barbu23 » 28 Fév 2009, 19:45
Bonsoir :
Pourquoi un système orthonormée
_{i \in I} $)
est libre ?
Merci d'avance de vos reponses ! :happy2:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 28 Fév 2009, 19:58
par barbu23 » 28 Fév 2009, 19:58
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités