Exercice sur les derivées

[Zineb]

Bonjour, alors voila j'ai un exercice a faire pour demain mais je bloque sur 3 questions. Votre aide me serrait précieuse.

soit la fonction f définie par f(x)=(-x^2+15x-9)/(x^2+9)
et cf sa courbe représentative dans un repère o i j d'unités 1 cm sur l'axe des abscisse et 2 cm sur l'axe des ordonnées

1°) b) déterminer les abscisses des points où la courbe cf coupe l'axe des abscisses (valeurs exactes)

c)
résoudre f(x)+1 = 0
(-x² + 15x - 9) / (x² + 9) + 1 = 0
(-x² + 15x - 9 + 1(x² + 9)) / (x² + 9) = 0
15x / (x² + 9) = 0
La fonction est nulle si son numérateur est nul, ça revient à résoudre :
15x = 0
S = {0}
f(0) + 1 = 0

or on me demande de faire l'intérprétation graphique que je ne sais pas vraiment faire


2°) b) exprimer f(x)+(7/2) en fonction de x
je trouve 5(x+3)^2 / 2(x^2+9)

en déduire que -7/2 est le minimum de f sur grand r
ca j'arrive pas

voila sinon j'ai fait tout le reste de l'exercice.

Merci beaucoup dans tous les cas

[marie49]

Salut

1. b.
La courbe Cf est l'ensemble des points de coordonnées (x, f(x))
L'axe des abscisses est l'ensemble des points de la forme (x,0)

Donc, pour trouver l'intersection de Cf avec l'axe des abscisses, il faut résoudre : f(x)=0

[....]
Je te laisse continuer, tu dois résoudre une équation du second degré.


1.c.
Tu viens de trouver tous les points x qui vérifient l'équation f(x) = -1
Donc, tu connais tous les points de la courbe de la forme (x,-1)
Graphiquement, si tu traces la droite d'équation y=-1, tu verras que Cf coupe cette droite une seule fois, au point d'abscisse x=0


2.b.

Dire que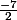 est le minimum de f sur signifie que :
Pour tout x dans ,
Ou encore que

Que peux-tu dire du signe de ?


Bon courage!