Exo de TS sur les suites

[Anonyme]

Ceci n'est pas un DM mais un exo que ma prof à qualifier de dur, et en le fesant je me suis rendu compte qu'elle avait raison, si vous pouviez me donner un coup de main


On considere 2 suite (Un) et (Vn) à termes positifs definies par U(0)=2 et V(0)=8 et par les relations de recurrences U(n+1)=[U(n)+V(n)]/2 et V(n+1)=racines de [U(n) x V(n)]

1° Montrer que pour n>0, V(n) << U(n) et que U(n) decroissante et V(n) croissante
2° demontrer que pour tout n>0 U(n+1) - V(n+1) << 0.5[U(n) - V(n)]
3° demontrer alors que pour tout n de N (entier naturel) U(n+1)-V(n+1)<< (0.5)^n
4° En deduire que les suites ont même limites



Voila mon exo, pour la 3 et la 4 je vois à peu pré le raisonement à suivre mais je n'arrive pas à debuter sur la 1°

Merci de me filer un petit coup de main ! (je represice que ce n'est pas un DM)

[Sphinx]

Salut!
1/- =( + )/2-
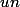=.5( - )^2
Il fallait quand même voir l'identité remarquable!
Ceci étant positif,> pour tout n.
2/ - < +
En multipliant les deux membres par -,on obtient ( -)^2<a-b
Encore une identité remarquable!
Tu n'as plus qu'à remplacer a par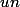 et b par .
3/Par récurrence.
- <0.5(-)<0.25(-) etc.
4/(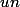 ) et ( ) sont deux suites adjacentes,elles convergent donc vers la même limite.

[Anonyme]

Merci !!

Effectivement je n'avais pas vu les identitées remarquable ce qui me bloqué
Par contre je comprend pas trop ton explication pour la 3° (je precise que je viens juste de commencer la recurrence donc je suis pas encore un pro, mais j'y travaille ^^

[Sphinx]

3/<1/2()
Donc <1/2()
Par conséquent,<1/2*1/2().
Tu peux ainsi remonter jusqu'à zéro,en multipliant chaque fois par 1/2.
Ce qui te donnera fatalement une puissance de 1/2.
Je te rappelle au passage que 1/2=0.5!
Toutefois,ce raisonnement n'est pas formel.
Aussi faut-il raisonner par récurrence.
Si <1/2^n,alors <1/2()<1/2*1/2^n=1/2^(n+1)
La propriété se transmet donc de n à n+1.
Il reste à prouver qu'elle est vraie pour n=0,soit que <1/2^0=1.
Je te laisse chercher.
Ciao et bonne continuation!

[Sphinx]

Pour ultime information,=5 et =4 ,donc - =1.