Exo d'olym

par **midouw** » 24 Fév 2009, 18:34

x et y deux chiffres strictement positifs
tel que x+y=8

montrez que (x+1/y)²+(y+1/x)²>=289/8

par **lapras** » 24 Fév 2009, 20:59

quelle olympiade ? c'est une application directe des moyennes
Moyenne quadratique/ arithmétique =>

Moyenne harmonique/arithmétique :

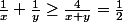
donc

par **midouw** » 24 Fév 2009, 22:17

lapras a écrit:quelle olympiade ? c'est une application directe des moyennes

Moyenne harmonique/arithmétique :

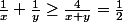
donc

Je vais paraître idiiot mais tant pis ... tu peux m'expliquer ce que t'as fait là ??

par **lapras** » 24 Fév 2009, 22:20

Pas grave !
J'ai juste utilisé la premiere inégalité que j'ai démontré (quadratique) et ajouté la seconde (harmonique).

par **midouw** » 24 Fév 2009, 22:24

Non ça j'avais compris (chui pas si débile que ça hein ^^")
Mais je suis débile en fait car je comprends pas la méthode que t'as utilisé pour la moyenne harmonique

par **lapras** » 24 Fév 2009, 22:29

Moyenne harmonique/arith. :
2/(1/x+1/y) <= (x+y)/2
je passe à l'inverse, je multiplie par 2 et j'obtiens 1/x+1/y >= 4/(x+y)

par **midouw** » 24 Fév 2009, 22:34

lapras a écrit:Moyenne harmonique/arith. :
2/(1/x+1/y) = 4/(x+y)

Bon là c'est la cata totale mais mieux vaut admettre sa bêtise parfois ... juste les trucs en gras que j'ai pas saisi

par **lapras** » 24 Fév 2009, 22:50

C'est moi qui ne doit pas être clair.
En fait il existe un théoreme entre les moyennes harmonique et arithmetique :

ici

:

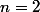
donc

Exo d'olym

Exo d'olym

Qui est en ligne