bonjour pourriez vous s'il vous plait m'aider pour l'étude de cette suite récurrente définie par u0=1 et Un+1=Un+2/Un
car f: x -> x+2/x est une fonction de R* dans R mais elle n'est pas monotone or je croyais que l'on ne pouvait avoir que deux cas soit f croissante soit f décroissante? merci d'avance pour votre aide
Suite récurrente
9 messages
- Page 1 sur 1
Bonjour,
ce n'est pas grave si f n'est pas monotone: elle est quand meme monotone par intervalles.
Quel est le point fixe ? Est ce que u0 se trouve avant ou apres le point fixe ? Est ce que f est croissante ou decroissante sur cet intervalle ?
Au fait, une precision, est ce que c'est bien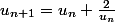 ? Il manque des parentheses dans ton expression
? Il manque des parentheses dans ton expression
ce n'est pas grave si f n'est pas monotone: elle est quand meme monotone par intervalles.
Quel est le point fixe ? Est ce que u0 se trouve avant ou apres le point fixe ? Est ce que f est croissante ou decroissante sur cet intervalle ?
Au fait, une precision, est ce que c'est bien
en faite je voudrais juste savoir pourquoi losque l'on applique la méthode ça ne marche pas car l'ensemble de définition de la fonction est bien R* et on a Uo=1 donc pour savoir si U est définie on a juste à regarder si f(Uo) appartient à R* ce qui est le cas
mais maintenant pour trouver la monotonie de U puis-je ne m'intéresser qu'a l'inervalle ]0,inf[? mais le problème c'est que sur cet intervalle f est décroissante puis croissante donc comment dois-je faire? merci d'avance
mais maintenant pour trouver la monotonie de U puis-je ne m'intéresser qu'a l'inervalle ]0,inf[? mais le problème c'est que sur cet intervalle f est décroissante puis croissante donc comment dois-je faire? merci d'avance
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
