Rayon de convergence

[Percolaptor]

Bonsoir

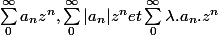
Concernant les séries entières, je ne comprends pas pourquoi avec €C* ont le meme rayon de convergence ?

Merci d'avance

[Joker62]

Haileau ;)
Critère de d'Alembert ???

[Percolaptor]

ok merci .
J'aurais une autre question, concernant un exemple du cours,
a pour rayon de convergence 1 car pour |z|<1, et est borné donc R|z| et R1
De plus, pour z=1, est non borné donc

Pourquoi est borné ?

[mathelot]

Pourquoi est borné ?

Bj,

soit


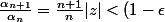car la limite du quotient est|z|

pour z fixé, |z|<1,

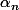
la suite de terme général , pour n assez grand,
est majorée en module par une suite géométrique convergente
de raison

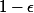
elle est cv (vers zéro), et bornée.

[Joker62]

Attention à bien faire la différence entre le critère de d'Alembert pour les séries entières et celui pour les séries numériques.

Ici Mathelot a bien fixé z et utilise donc celui pour les séries numériques.

[ThSQ]

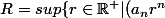Retour aux sources : bornée

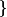
(a_n r^n) bornée (|a_n| r^n) bornée ...

[Lemniscate]

Pourquoi est borné ?

Si 0 < |z| < 1 , n|z|^n = n.exp(n.ln(|z|)) donc converge vers 0 par croissance comparées donc est bornée ! Si z=0 c bon aussi !

[Percolaptor]

Bonjour,
concernant la définition du rayon de convergence, ici r=z ?

[Lemniscate]

Bonjour,
concernant la définition du rayon de convergence, ici r=z ?

Ici R = 1 parce que la suite est bornée (ou la série cv c comme tu veux) ssi |z| < 1.

[Percolaptor]

je ne comprends pas la définition du rayon de convergence :
est ce que R = bornee }
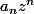
ca signifie que pour tout z€C, |z| bornée
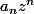
et pour tout z€C, |z|>R non bornée ?

[Lemniscate]

je ne comprends pas la définition du rayon de convergence :
est ce que R = bornee }
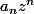
ca signifie que pour tout z€C, |z| bornée
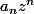
et pour tout z€C, |z|>R non bornée ?

Oui c cela.

Mais tu peux "définir" de manières équivalentes le rayon de cv comme :

R = bornee }
R = converge }
R = converge }
R = converge absolument}
R = diverge}

Merci de modifier si ce que j'ai dit est faux, je peux m'être trompé, mais grosso modo tu as plusieurs définitions équivalentes...

[Joker62]

En fait tout part du Lemme d'Abel

En se donnant une série entière si on a a_n.p^n bornée alors tout les z dans C de module strictement plus petit que p, on a a_n.z^n converge absolument

A partir de là on peut définir le rayon de convergence R comme le sup des p

[Percolaptor]

ok merci

ok merci .
J'aurais une autre question, concernant un exemple du cours,
a pour rayon de convergence 1 car pour |z|<1, et est borné donc R|z| et R1
De plus, pour z=1, est non borné donc

je ne comprends toujours pas pourquoi R|z|. Car d'apres le théoreme précédent, |z|<1 ssi est borné donc on peut tout de suite dire que R=1 non?

[Lemniscate]

Revois juste la notion de borne sup :)