Probleme dérivée

[fabio123]

bonjour,

je rencontre un problème lors de la démo suivante:

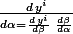
(eq°1)

ce qui donne:

(eq°2)

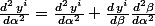
si je simplifie le premier terme de l'eq n°2, je me retrouve avec : (eq°3)

ce qui mène à :



ceci est le résultat voulu mais l'équation n°2 est elle mathématiquement correcte ? car il y a deux termes identiques de chaque coté

merci pour votre aide.

[mathelot]

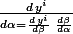
(eq°1)

on dérive par rapport à une variable et on multiplie par
la dérivée de relativement à

au deuxième ordre, cet algorithme (dérivée composée) donne

(eq°2)

ce qui n'est pas le même résultat que le tien.

après, je me suis demandé si, dans le cas où la relation liant
et est de classe C2,
est ce que l'on peut inverser l'ordre des dérivations dans
ce qui donnerait zéro ?

[mathelot]

La notion de fonction est très souple et purement ensembliste.
Par exemple, si l'on sait que la galaxie du Centaure ne cesse de s'éloigner
de la Terre et que les cours des actions à Wall Street ne cessent de baisser,
un jardinier peut constater que la hauteur de ses rosiers
est fonction de la distance de la Terre au Centaure et des cours de bourse.

c'est toujours ce que j'explique (en une variable) à mes élèves de Seconde.
Ainsi, si l'on étudie n quantités dont les mesures fournissent n variables,
le théorème des fonctions implicites donne, pour règle générale,
que ,localement, c'est-à-dire si les variations restent petites, les variables sont alors liées par des relations fonctionnelles (de type fonction), fonctions dérivables.

Ce qui explique pourquoi on peut composer pratiquement à l'infini
et dériver dans tous les sens. Les ennuis ne sont pas là. Ils commencent
quand on cesse d'être protégé par le théorème des fonctions implicites
et que les variables varient beaucoup, disons , en dehors
de voisinages choisis pour leur arbitraire petitesse.

Alors on voit apparaitre des contraintes d'ordre topologique comme
de faire varier les quantités dans un ouvert convexe,étoilé,simplement connexe,connexe ou pire sur des sous-variétés affines.