Nombre periodique

[fourize]

bonjour;

je suis actuellement sur l'arithmétique, que je trouve très astucieux,
et j'aimerai solliciter votre aide sur un devoir, plus précisément sur l'exercice 2,
petit (1) et (3).voir ici
http://www.cmi.univ-mrs.fr/~coulbois/2009/arithmetique/devoir1-ma403-2009.pdf

l'exercice 1. ça va; par contre l'exo 2; ce qui me pose problème c'est comment trouver (1°) et le (3°)
desesperement j'avais commencé par multiplier 17,2433333 par 3 mais je ne vois pas ou est ce que je peux en venir avec :triste:

merci d'avance de m'avoir lu?

[Djeordjes]

Bonsoir
Soit A=17,24333333....

On a 1000xA =...

Pour la question 3, sans l'avoir faite proprement, avec la division euclidienne du numérateur, puis des restes par le dénominateur, ne peux tu pas t'en sortir ?

Bon courage

[fourize]

Bonsoir
Soit A=17,24333333....
On a 1000xA =...

tout d'abord merci de m'avoir répondu mais je vois pas du tout ce que tu veux dire par la? l'exercice demande de trouver l'écriture de la forme a/b de 17,2433333 ?
si je multiplie A*1000 = 172433,3333333 je m'en sort pas ???

Pour la question 3, sans l'avoir faite proprement, avec la division euclidienne du numérateur, puis des restes par le dénominateur, ne peux tu pas t'en sortir ?
Bon courage

que ce que tu entend par "l'avoir faite proprement?". on veut demontrer quelque chose. et on n'a pas des applications numerique ??

:marteau:

[uztop]

Bonjour,

je trouve l'énoncé un peu bizarre:
17.24333333.... est périodique de période 1, pas 3 (le chiffre 3 se répète à chaque fois, donc à 1 d'intervalle)
Sinon, pour la forme rationnelle, multiplier par 3 me semble une bonne idée. Dans la définition de l'écriture décimale, on a

"Pour assurer l’unicité de l’écriture décimale on suppose de plus que cn 6= 0 et que la suite de chiffres (dk) n’est pas ultimement constante égale à b 1."

: ça signifie que
0,xxx99999999999999... = 0,xxy avec y=x+1

Pour l'écriture décimale de 7/250, il suffit de faire la division euclidienne (la division comme au primaire), on trouve assez facilement que le résultat est périodique

Pour la 3, ça se démontre effectivement par la division euclidienne.
On divise P par Q, à chaque étape de la division euclidienne, on va obtenir un reste qui est compris entre 0 et 10Q (par définition de la division euclidienne); étant donné que l'opération se répète un nombre infini de fois, on tombe nécessairement sur deux restes identiques; le résultat est donc périodique.

[fourize]

ouf, tu me rassure;

Bonjour,
Sinon, pour la forme rationnelle, multiplier par 3 me semble une bonne idée. Dans la définition de l'écriture décimale, on a : ça signifie que
0,xxx99999999999999... = 0,xxy avec y=x+1

au fait, sur la dexieme partie de cette question j'ai bien fait la division, pas de souci. mais sur cette première partie en multipliant par 3 je trouve:
51,7299999 après je ne sais pas quoi faire.
dans ta théorie y=x+1, qui est x et qui est Y. d'ailleurs j'ai pas 0,xxy plutôt 0,xyzzzzzz. tu m'expliquais un peu plus (merci)

Pour la 3, ça se démontre effectivement par la division euclidienne.
On divise P par Q, à chaque étape de la division euclidienne, on va obtenir un reste qui est compris entre 0 et 10Q (par définition de la division euclidienne); étant donné que l'opération se répète un nombre infini de fois, on tombe nécessairement sur deux restes identiques; le résultat est donc périodique.

je pense que je peux faire maintenant la 3 grace à toi .
mais j'avais utilisé cette méthode pour exo2_2 y aurait t'il pas une confusion.

par ailleurs, j'avais continué l'exercice 3 en attendant, sur ce je me suis bloquer à la dernière question. le 5 ???

cordialement,
fourize.

[uztop]

en fait la convention dont je te parle est la suivante: 0,99999999999..... = 1 qui est valable quand on a une infinité de 9.
Dans mon exemple, x est un nombre quelconque, c'est juste pour dire qu'on est pas obligé de commencer par 0,9999..... mais on peut aussi dire 0,19999999.... =0,2 par exemple.

Quelle est la démo que tu as utilisé pour la question 2-2 ? La démo que je te propose montre qu'un nombre rationnel a un développement décimal périodique, ce qui correspond bien à la question 3. Pour la 2, il faut montrer la réciproque.

[fourize]

re

en fait la convention dont je te parle est la suivante: 0,99999999999..... = 1 qui est valable quand on a une infinité de 9.
Dans mon exemple, x est un nombre quelconque, c'est juste pour dire qu'on est pas obligé de commencer par 0,9999..... mais on peut aussi dire 0,19999999.... =0,2 par exemple.

OUAIS! j'ai compris ta convention mais en quoi ça nous arrange?
j'aurai 17,2433333*3 = 51,73 (qui n'est pas une fraction et je ne vois pas trop comment la transformer en fraction :triste: ???)

Quelle est la démo que tu as utilisé pour la question 2-2 ? La démo que je te propose montre qu'un nombre rationnel a un développement décimal périodique, ce qui correspond bien à la question 3. Pour la 2, il faut montrer la réciproque.

pour ce que t'appelle réciproque, ça m'a l'aire de ce qu'on fait avec le 17,2433333 mais je vois pas trop comment?
je me donne un nombre périodique et j'essaie de montrer qu'il peu s'écrire sous forme rationnel, c'est ça?

[Doraki]

tu n'arrives pas à voir que 51,73 est une fraction ?
et 0,1 non plus ?

sinon, je préfère multiplier un nombre comme 0.3333... par (10-1) plutôt que par 3 pour montrer qu'il est rationnel.

[Djeordjes]

Re bonjour.

Effectivement, je m'ai trompé, c'est 100xA que tu peux très facilement écrire sous forme de fraction, et du coup, A lui même... Mais bon, l'idée est la même, et cela marche avec 1000 aussi

Et pour la question 2, c'est la même chose :
Soit e le nombre périodique de période T, de préfixe p, de partie périodique q
est composé d'une partie entière, et d'une partie décimale "tout de suite périodique", c'est à dire de préfixe 0.
Soit d cette partie décimale (la partie entière se met bien sous forme de fraction, hein ? )
Alors ce qui te permet d'avoir une écriture fractionnaire de d, et donc de e...
Voilà, je crois que c'est fait à peu près proprement, plus proprement, tu n'aurais rien à faire

Essaie de réfléchir à ce que j'écris avant de me donner des coups de maillets

@uztop : On dit effectivement que 17,543333... est périodique de période 1 de partie périodique 3... Tout comme 0,345345345... est périodique de période 3 de partie périodique 345

[uztop]

Bon alors rapidement, je suis au travail et je ne suis pas sense faire des maths
51,73 = 5173/100 et est donc bien une fraction (c'est d'ailleurs ce qu'a dit Djeordjes)

Pour la question 2, il faut partir d'un nombre periodique A (considerons qu'il a prefixe P avec n chiffres apres la virgule et est ensuite periodique de periode T)
Sa partie periodique est , on a donc:
On a donc
On reconnait la somme des termes d'une suite geometrique, le resultat peut donc se simplifier et on trouve une ecriture rationnelle de A

@Djeordjes Merci de m'avoir confirme les definitions de periode et partie periodique

[fourize]

bonjour,

maintenant l'exercice 2. je l'ai reussi, grâce à vous sans doute!(merci de vos explication)
mais je suis actuellement au petit 1 de lexo 3.
et j'ai bloque des le début ça me parait bizarre, :dodo:

par quoi commencer (pas de resultats juste le tuyau, j'adore gribouiller )

[uztop]

la question 1 du 3 ?
Il suffit de faire la division Euclidienne; qu'est ce qui te pose probleme exactement ?

[fourize]

bonjour;

la question 1 du 3 ?
Il suffit de faire la division Euclidienne; qu'est ce qui te pose probleme exactement ?

désolé uztop. je me suis trompé c'est à partir du 2 du 3 que je bloque;-).
plus precisement les pistes pour les demos. (merci)

=> si je ne sais pas faire une division euclideienne; que ce que je fais en sup?<=

[uztop]

bonjour;



désolé uztop. je me suis trompé c'est à partir du 2 du 3 que je bloque;-).
plus precisement les pistes pour les demos. (merci)

=> si je ne sais pas faire une division euclideienne; que ce que je fais en sup?<=

ah tu me rassures :we:
Je vais regarder ce soir, je n'ai vraiment pas le temps maintenant, desole

[uztop]

Bon, une idée de démonstration serait:
(c'est l'écriture de x en base b, avec un nombre fini de termes).
se décompose en produit de facteurs premiers .
Si on met tout au même dénominateur (donc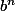 ) dans la deuxième expression on voit que pour que l'égalité soit vraie, b doit diviser les .
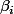Il manque surement des trucs mais je pense que c'est un point de départ comme démonstration.

[fourize]

bonsoir,

en procèdant que tu dis: suivie d'une identification; on obtient

est ce on pourra dire que ça divise b??? (je comprendrai si on prend k=1/ )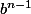

par contre sur ton ecriture en base b de X, d'ou vient ces plus.
je sais bien que 8 = 100 ( en bas deux)?? ceci est un exemple. :briques:

[uztop]

si on a = les facteurs premiers de beta, alors on peut diviser de part et d'autre par un et le résultat obtenu reste entier : divise , il divise donc b ( est premier, on peut donc appliquer le lemme d'Euclide)

En ce qui concerne mon écriture de x en base b, c'est la définition.
10,23 en base 10 =

[fourize]

presque fini

j'en suis au l'exercice3_3 .
moi j'ai fais:
comme divise

et ... et je bloque :triste:

d'abord, suis je dans le bon tuyau?
je n'arrive pas à comprendre ce que ça veut dire :
"la longueur de la periode de l'ecriture en base b de x divise T."

cordialement;

[fourize]

presque fini
j'en suis au l'exercice3_3 .
moi j'ai fais:
comme divise

et ... et je bloque :triste:
d'abord, suis je dans le bon tuyau?

est ce quelqu'un pourrait jeter un coup d'oeil avant que je continue ?

[uztop]

j'aimerais t'aider mais je ne suis pas sûr de comprendre la question: c'est quoi la longueur de la période ? T est la période (qui est la longueur de la partie périodique), mais la longueur de T, je ne vois pas du tout quel renseignement on a dessus ...