Une intégrale

par **Pythales** » 13 Fév 2009, 17:37

Bonjour
J'essaye de calculer par les moyens "classiques" l'intégrale

Le calcul est facile par la méthode des résidus, et donne

(pour

), mais j'aimerais y arriver autrement
Merci d'avance

par **JUVENTINI** » 13 Fév 2009, 17:55

CHERCHER UNE EQUATION DIFFERENTIELLE VERIFIEE PAR f(x)=ton intégrale

par **Pythales** » 13 Fév 2009, 18:32

J'y ai pensé ...

par **Pythales** » 13 Fév 2009, 18:37

Excusez moi. La valeur est

...

par **Nightmare** » 13 Fév 2009, 19:00

Essaye de montrer que f''=f.

:happy3:

par **Pythales** » 13 Fév 2009, 19:09

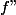
n'est pas convergente.

par **Nightmare** » 13 Fév 2009, 19:13

Et pourtant elle l'est.

par **ThSQ** » 13 Fév 2009, 19:20

Pythales a écrit:

Étrange pour une fonction visiblement paire non ?

par **Nightmare** » 13 Fév 2009, 19:22

C'est pour x > 0 ThSQ !

Autrement, sur R*, on rajoute une valeur absolue au x.

par **Pythales** » 13 Fév 2009, 19:23

Exact. Pour

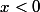
elle vaut

par **ThSQ** » 13 Fév 2009, 19:26

Nightmare a écrit:C'est pour x > 0 ThSQ !

Autrement, sur R*, on rajoute une valeur absolue au x.

Oui oui, je viens de lire ça :marteau: :mur:

par **Maxmau** » 14 Fév 2009, 10:33

Bonjour
f(x) ton intégrale
F(x) une primitive
cherche une équa diff dont F est solution

par **Pythales** » 14 Fév 2009, 10:57

Ca marche. Merci. Dire que j'étais passé tout près du résultat !

par **rabab** » 14 Fév 2009, 22:23

tu peux aussi utiliser les séries de Fourier