Problème de calcul tangente

[pikmin]

Bonjour,

je dois calculer des tangentes en 0+ et 0- de

j'ai essayé avec la formule f(x)-f(a)/x-a mais je n'arrive pas aux résultats prévus qui doivent être respectivement 0 et -1

merci d'avance pour votre aide

[XENSECP]

Les tangentes ou les coefficients directeurs ?

[mathelot]

bonjour,

j'ai (un peu) la flemme de faire les calculs:

1ère méthode

avec le taf, on regarde

poser

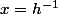
si cette limite existe, elle vaut le nombre dérivé

2ème méthode

il se peut que cette limite n'existe pas, mais que
existe si f' n'est pas continue.

à ce moment là étudier , toujours en posant

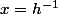
[pikmin]

Les tangentes ou les coefficients directeurs ?

euh oui j'ai oublié de préciser, ce sont les coefficients directeurs que je souhaite trouver

[phryte]

Bonjour.
f(x) = 1/(exp(1/x)-1)
f'(x)= exp(1/x)/(x^2(exp(1/x)-1)^2
Pour X = 1/x et x--> 0 + X --> +inf
f'(X) --> 0
Le coefficient angulaire en 0+ est = 0
Pour 0- f(x) --> -1 et f'(x) --> 0 en f(x) = -1
Donc les coefficients angulaire sont les mêmes = 0 mais il y a une discontinuité en 0